filmov
tv
Extended Euclidean Algorithm

Показать описание
We reverse the Euclidean Algorithm to find values of x and y so that gcd(a,b)=ax+by.
The Extended Euclidean algorithm
Extended Euclidean Algorithm (Solved Example 1)
Extended Euclidean Algorithm and Inverse Modulo Tutorial
Extended Euclidean Algorithm Example
Extended Euclidean Algorithm - Example (Simplified)
Extended Euclidean Algorithm
Number Theory | Extended Euclidean Algorithm Example #1
Extended Euclidean Algorithm Explained
Number Theory | Extended Euclidean Algorithm Example 2
The extended Euclidean algorithm in one simple idea
Extended Euclidean Algorithm
Extended Euclidean Algorithm (Solved Example 2)
Extended Euclidean Algorithm
Extended Euclid Algorithm - Number Theory Advanced | C++ Placement Course | Lecture 37.1
Extended Euclidean Algorithm (Solved Example 3)
An Example of GCD, and Extended Euclidean Algorithm In Finding the Bezout Coefficients
Extended Euclidean Algorithm in Cryptography | Abhishek Sharma
Extended Euclidean Algorithm using Example Multiplicative inverse of a number | Cryptography
GCD, Bezout, and Modular Inverses | The Extended Euclidean Algorithm
Extended Euclidean Algorithm: GCD is a Linear Combination
Extended Euclid Algorithm to solve 201x+81y=3
Extended Euclidean Algorithm - Cryptography - Cyber Security - CSE4003
GCD Algorithms | (Part 2)Extended GCD Algorithm | CodeChef Tutorials
Bézout's identity: ax+by=gcd(a,b)
Комментарии
 0:12:11
0:12:11
 0:10:16
0:10:16
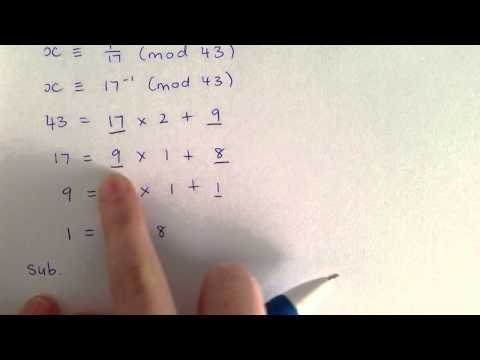 0:06:00
0:06:00
 0:14:50
0:14:50
 0:07:40
0:07:40
 0:02:42
0:02:42
 0:08:53
0:08:53
 0:06:21
0:06:21
 0:12:13
0:12:13
 0:10:59
0:10:59
 0:10:50
0:10:50
 0:05:43
0:05:43
 0:11:54
0:11:54
 0:09:18
0:09:18
 0:06:54
0:06:54
 0:00:59
0:00:59
 0:11:19
0:11:19
 0:04:24
0:04:24
 0:22:21
0:22:21
 0:04:09
0:04:09
 0:05:46
0:05:46
 0:14:34
0:14:34
 0:11:03
0:11:03
 0:18:20
0:18:20