filmov
tv
Extended Euclidean Algorithm (Solved Example 1)

Показать описание
Network Security: Extended Euclidean Algorithm (Solved Example 1)
Topics discussed:
1) Explanation on the basics of Multiplicative Inverse for a given number under modulus.
2) Introduction to Extended Euclidean Algorithm to find the Multiplicative Inverse.
3) Steps and working of the Extended Euclidean Algorithm to find the Multiplicative Inverse.
4) Solved example to find the Multiplicative Inverse using Extended Euclidean Algorithm.
5) Explanation of how to verify the Multiplicative Inverse.
Music:
Axol x Alex Skrindo - You [NCS Release]
#NetworkSecurityByNeso #Cryptography #NetworkSecurity #ExtendedEuclideanAlgorithm
Topics discussed:
1) Explanation on the basics of Multiplicative Inverse for a given number under modulus.
2) Introduction to Extended Euclidean Algorithm to find the Multiplicative Inverse.
3) Steps and working of the Extended Euclidean Algorithm to find the Multiplicative Inverse.
4) Solved example to find the Multiplicative Inverse using Extended Euclidean Algorithm.
5) Explanation of how to verify the Multiplicative Inverse.
Music:
Axol x Alex Skrindo - You [NCS Release]
#NetworkSecurityByNeso #Cryptography #NetworkSecurity #ExtendedEuclideanAlgorithm
Extended Euclidean Algorithm (Solved Example 1)
Extended Euclidean Algorithm (Solved Example 2)
Extended Euclidean Algorithm (Solved Example 3)
Extended Euclidean Algorithm Example
Extended Euclidean Algorithm - Example (Simplified)
The Extended Euclidean algorithm
Extended Euclidean Algorithm and Inverse Modulo Tutorial
Number Theory | Extended Euclidean Algorithm Example 2
The extended Euclidean algorithm in one simple idea
Extended Euclidean Algorithm
An Example of GCD, and Extended Euclidean Algorithm In Finding the Bezout Coefficients
Extended Euclidean Algorithm
GCD, Bezout, and Modular Inverses | The Extended Euclidean Algorithm
Extended Euclidean Algorithm to Solve Linear Diophantine Equation
Euclidean Algorithm - An example ← Number Theory
Chapter 1 - Extended Euclid Algorithm example 2 : 85 and 37
Extended Euclidean Algorithm Explained
Worked Example: Extended Euclidean Algorithm
Extended Euclidean Algorithm to find the Inverse Example 1 - Part 2
Extended Euclidean Algorithm Example
Extended Euclidean Algorithm
Extended Euclidean Algorithm using Example Multiplicative inverse of a number | Cryptography
Euclidean algorithm to find GCD of two number
Linear Diophantine equations and the extended Euclidean algorithm - 1st year student lecture
Комментарии
 0:10:16
0:10:16
 0:05:43
0:05:43
 0:06:54
0:06:54
 0:14:50
0:14:50
 0:07:40
0:07:40
 0:12:11
0:12:11
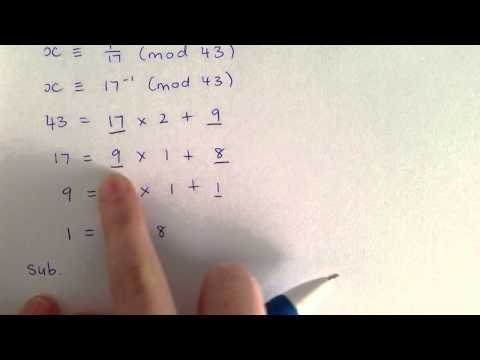 0:06:00
0:06:00
 0:12:13
0:12:13
 0:10:59
0:10:59
 0:08:48
0:08:48
 0:00:59
0:00:59
 0:02:42
0:02:42
 0:22:21
0:22:21
 0:00:59
0:00:59
 0:02:04
0:02:04
 0:07:32
0:07:32
 0:06:21
0:06:21
 0:18:14
0:18:14
 0:09:02
0:09:02
 0:15:42
0:15:42
 0:11:54
0:11:54
 0:04:24
0:04:24
 0:05:15
0:05:15
 0:48:42
0:48:42