filmov
tv
Derivative of x^x^x - Logarithmic Differentiation of Exponential Functions
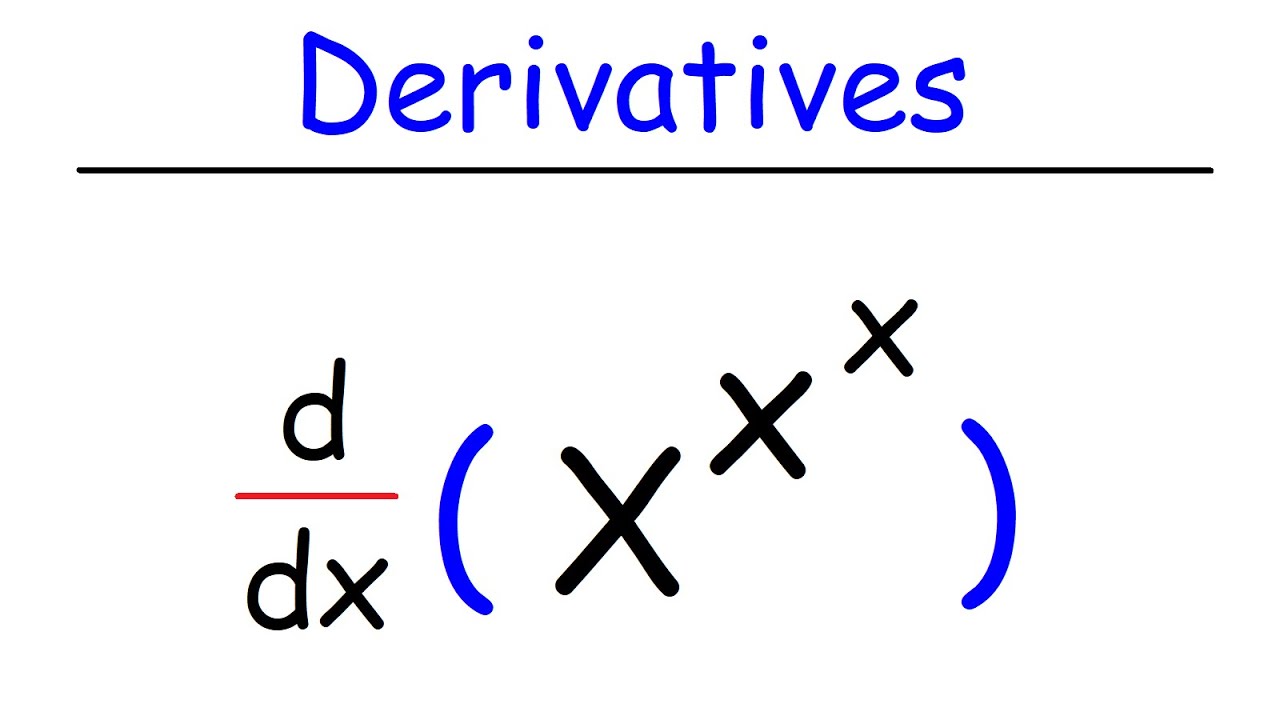
Показать описание
This calculus video explains how to find the derivative of x^x^x using logarithmic differentiation which is useful for differentiating exponential functions with a variable in the exponent position.
Derivatives - The Product Rule - f*g:
Derivatives - The Quotient Rule:
Derivatives - The Chain Rule:
Derivatives - Composite Functions:
__________________________________
Implicit Differentiation:
Derivatives of Inverse Trig Functions:
Derivatives of Exponential Functions:
Derivatives of Logarithmic Functions:
Logarithmic Differentiation:
___________________________________
Derivatives - Using Logarithms:
Derivatives of Inverse Functions:
Derivatives - Differentiation Rules:
Derivatives - Function Notations:
Derivatives - The Reciprocal Rule:
_________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Derivatives - Formula Sheet:
Derivatives - The Product Rule - f*g:
Derivatives - The Quotient Rule:
Derivatives - The Chain Rule:
Derivatives - Composite Functions:
__________________________________
Implicit Differentiation:
Derivatives of Inverse Trig Functions:
Derivatives of Exponential Functions:
Derivatives of Logarithmic Functions:
Logarithmic Differentiation:
___________________________________
Derivatives - Using Logarithms:
Derivatives of Inverse Functions:
Derivatives - Differentiation Rules:
Derivatives - Function Notations:
Derivatives - The Reciprocal Rule:
_________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Derivatives - Formula Sheet:
Комментарии
 0:11:46
0:11:46
 0:12:13
0:12:13
 0:04:43
0:04:43
 0:08:41
0:08:41
 0:00:43
0:00:43
 0:13:31
0:13:31
 0:03:02
0:03:02
 0:12:03
0:12:03
 0:02:45
0:02:45
 0:05:15
0:05:15
 0:01:23
0:01:23
 0:07:54
0:07:54
 0:02:59
0:02:59
 0:00:30
0:00:30
 0:05:14
0:05:14
 0:16:49
0:16:49
 0:00:52
0:00:52
 0:02:15
0:02:15
 0:02:47
0:02:47
 0:01:53
0:01:53
 0:02:44
0:02:44
 0:03:16
0:03:16
 0:01:01
0:01:01
 0:03:08
0:03:08