filmov
tv
#219. БИНОМ НЬЮТОНА ДЛЯ ЧАЙНИКОВ

Показать описание
Вы знаете, почему 0!=1? В любом случае: пора разобраться с азами комбинаторики и с одной из самых известных формул в математике — биномом Ньютона!
Все мы помним сокращенного умножения, в частности, квадрат суммы (a+b)²=a²+2ab+b² и куб суммы (a+b)³=a³+3a²b+3ab²+b³. Но не всем посчастливилось узнать, как же работает формула (a+b)ⁿ в общем виде. Вот этот промах мы сейчас и устраним! Чаще всего это тождество доказывают по индукции. Мы же зайдем скорее со стороны комбинаторики, индукция пройдет почти незаметно. Перестановки и сочетания прилагаются!
0:00 — Интро
0:15 — Геометрические интерпретации
1:29 — Перестановки
3:03 — Сочетания
4:54 — Бином Ньютона
6:44 — Бонусы
В момент 6:28 (2π так сказать) опечатка: в знаменателе должно быть 0!∙(5-0)!
ВОПРОС. Почему мы 20 делили на 2?
ОТВЕТ. Сколькими способами можно выбрать два элемента из четырех?
Частное 4!/2! дает результат 12. Частное 4!/(2! ∙ 2!) дает результат 6. Какой же из этих ответов верен и почему?
Рассмотрим множество {A, Б, В, Г} и выпишем явно всевозможные пары:
1) {А, Б}
2) {А, В}
3) {А, Г}
4) {Б, В}
5) {Б, Г}
6) {В, Г}
Получили шесть пар, что соответствует второму варианту. Именно в нем делением на (n-k)!=(4-2)! мы отразили то, что {А, Б} и {Б, А} для нас одно и то же. Мы делили дополнительно на 2!, то есть на количество способов переставить два элемента
БОЛЬШЕ ИНТЕРЕСНОЙ МАТЕМАТИКИ
#Математика #Наука #Научпоп
Все мы помним сокращенного умножения, в частности, квадрат суммы (a+b)²=a²+2ab+b² и куб суммы (a+b)³=a³+3a²b+3ab²+b³. Но не всем посчастливилось узнать, как же работает формула (a+b)ⁿ в общем виде. Вот этот промах мы сейчас и устраним! Чаще всего это тождество доказывают по индукции. Мы же зайдем скорее со стороны комбинаторики, индукция пройдет почти незаметно. Перестановки и сочетания прилагаются!
0:00 — Интро
0:15 — Геометрические интерпретации
1:29 — Перестановки
3:03 — Сочетания
4:54 — Бином Ньютона
6:44 — Бонусы
В момент 6:28 (2π так сказать) опечатка: в знаменателе должно быть 0!∙(5-0)!
ВОПРОС. Почему мы 20 делили на 2?
ОТВЕТ. Сколькими способами можно выбрать два элемента из четырех?
Частное 4!/2! дает результат 12. Частное 4!/(2! ∙ 2!) дает результат 6. Какой же из этих ответов верен и почему?
Рассмотрим множество {A, Б, В, Г} и выпишем явно всевозможные пары:
1) {А, Б}
2) {А, В}
3) {А, Г}
4) {Б, В}
5) {Б, Г}
6) {В, Г}
Получили шесть пар, что соответствует второму варианту. Именно в нем делением на (n-k)!=(4-2)! мы отразили то, что {А, Б} и {Б, А} для нас одно и то же. Мы делили дополнительно на 2!, то есть на количество способов переставить два элемента
БОЛЬШЕ ИНТЕРЕСНОЙ МАТЕМАТИКИ
#Математика #Наука #Научпоп
Комментарии
 0:07:26
0:07:26
 0:03:27
0:03:27
 0:12:30
0:12:30
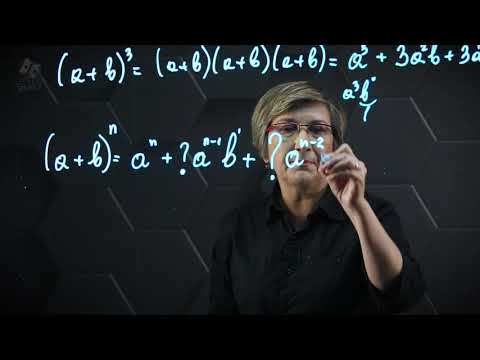 0:11:47
0:11:47
 0:03:56
0:03:56
 0:03:36
0:03:36
 0:19:02
0:19:02
 0:10:27
0:10:27
 0:01:00
0:01:00
 0:01:50
0:01:50
 0:09:20
0:09:20
 0:01:19
0:01:19
 0:00:16
0:00:16
 0:49:50
0:49:50
 0:09:45
0:09:45
 0:14:40
0:14:40
 0:14:35
0:14:35
 0:11:44
0:11:44
 0:09:44
0:09:44
 0:05:40
0:05:40
 0:10:27
0:10:27
 0:14:43
0:14:43
 0:00:51
0:00:51
 0:09:04
0:09:04