filmov
tv
Бином Ньютона: формула, доказательство и Треугольник Паскаля

Показать описание
Бином Ньютона — это формула, которая обобщает привычные нам формул сокращённого умножения (квадрат суммы и куб суммы, например). С помощью Бинома Ньютона можно разложить на слагаемые любую степень суммы. При этом у начинающих учеников возникает несколько проблем:
1. Формула Бинома Ньютона содержит знак суммы — это компактная запись множества слагаемых специального вида;
2. Сами слагаемые тоже не простые. Там есть степени (и это не проблема), а есть биноминальные коэффициенты;
3. Доказательство формулы Бинома Ньютона — отдельная история. Существует несколько способов доказать её, но мы будем опираться на метод математической индукции.
Таким образом, из этого урока вы узнаете:
1. Что такое Бином Ньютона, как выглядит эта формула, что с ней можно делать и что она вообще означает;
2. Что такое биноминальные коэффициенты. Как считается число сочетаний из n элементов по k элементов, при чём тут факториалы и комбинаторика;
3. Кстати, о факториалах. Мы дополним стандартное определение факториала с помощью рекуррентных формул. В частности, 0! = 1 — прямо по определению. Это ни в коем случае не противоречит "классическому" определению факториала (произведение всех натуральных чисел от 1 до n), но позволяет легко считать большие биноминальные коэффициенты;
4. Затем мы рассмотрим важнейшее свойство биноминальных коэффициентов, на основе которого построим треугольник Паскаля — ещё одну замечательную конструкцию, которую можно использовать для разложения степеней в многочлены даже в том случае, если вы не знаете, что такое Бином Ньютона;
5. Ну и вишенка на торте — мы докажем саму формулу Бинома Ньютона, опираясь на свойства биноминальных коэффициентов и математическую индукцию.
6. А в качестве опции рассмотрим более наглядный метод группировки слагаемых. После чего станет понятно, почему они группируются именно так, как предложено в доказательстве, а никак иначе.:)
В целом хочу отметить, что тема Бинома Ньютона — большая и сложная. Её нельзя объяснить и доказать в коротком видео. Точнее, объяснить-то как раз можно, но доказать — тут нужно детально разобраться в каждом элементе формулы. Поэтому видео получилось довольно объёмным, но при этом максимально полным и информативным.:)
00:00 0. Формула бинома Ньютона
01:55 1. Значок суммы
10:30 2. Биноминальные коэффициенты
16:25 3. Треугольник Паскаля
23:37 4. Доказательство Бинома Ньютона
42:08 5. Другой способ суммирования
Меня зовут Павел Бердов, и я веду этот канал для тех, кто изучает школьную математику 7—11 классов (алгебра, геометрия и стереометрия), готовится к профильному ЕГЭ по математике (или ОГЭ), а также изучает высшую математику в университете (в т.ч. уровня мехмата МГУ). Помимо теории предлагаю вашему вниманию задачи для самостоятельного решения. Поэтому смотрите, изучайте, решайте — и сдавайте экзамены и контрольные работы на пятёрки.:)
1. Формула Бинома Ньютона содержит знак суммы — это компактная запись множества слагаемых специального вида;
2. Сами слагаемые тоже не простые. Там есть степени (и это не проблема), а есть биноминальные коэффициенты;
3. Доказательство формулы Бинома Ньютона — отдельная история. Существует несколько способов доказать её, но мы будем опираться на метод математической индукции.
Таким образом, из этого урока вы узнаете:
1. Что такое Бином Ньютона, как выглядит эта формула, что с ней можно делать и что она вообще означает;
2. Что такое биноминальные коэффициенты. Как считается число сочетаний из n элементов по k элементов, при чём тут факториалы и комбинаторика;
3. Кстати, о факториалах. Мы дополним стандартное определение факториала с помощью рекуррентных формул. В частности, 0! = 1 — прямо по определению. Это ни в коем случае не противоречит "классическому" определению факториала (произведение всех натуральных чисел от 1 до n), но позволяет легко считать большие биноминальные коэффициенты;
4. Затем мы рассмотрим важнейшее свойство биноминальных коэффициентов, на основе которого построим треугольник Паскаля — ещё одну замечательную конструкцию, которую можно использовать для разложения степеней в многочлены даже в том случае, если вы не знаете, что такое Бином Ньютона;
5. Ну и вишенка на торте — мы докажем саму формулу Бинома Ньютона, опираясь на свойства биноминальных коэффициентов и математическую индукцию.
6. А в качестве опции рассмотрим более наглядный метод группировки слагаемых. После чего станет понятно, почему они группируются именно так, как предложено в доказательстве, а никак иначе.:)
В целом хочу отметить, что тема Бинома Ньютона — большая и сложная. Её нельзя объяснить и доказать в коротком видео. Точнее, объяснить-то как раз можно, но доказать — тут нужно детально разобраться в каждом элементе формулы. Поэтому видео получилось довольно объёмным, но при этом максимально полным и информативным.:)
00:00 0. Формула бинома Ньютона
01:55 1. Значок суммы
10:30 2. Биноминальные коэффициенты
16:25 3. Треугольник Паскаля
23:37 4. Доказательство Бинома Ньютона
42:08 5. Другой способ суммирования
Меня зовут Павел Бердов, и я веду этот канал для тех, кто изучает школьную математику 7—11 классов (алгебра, геометрия и стереометрия), готовится к профильному ЕГЭ по математике (или ОГЭ), а также изучает высшую математику в университете (в т.ч. уровня мехмата МГУ). Помимо теории предлагаю вашему вниманию задачи для самостоятельного решения. Поэтому смотрите, изучайте, решайте — и сдавайте экзамены и контрольные работы на пятёрки.:)
Комментарии
 0:07:26
0:07:26
 0:03:27
0:03:27
 0:49:50
0:49:50
 0:03:36
0:03:36
 0:03:56
0:03:56
 0:12:30
0:12:30
 0:01:50
0:01:50
 0:18:37
0:18:37
 0:30:13
0:30:13
 0:33:31
0:33:31
 0:12:38
0:12:38
 0:13:00
0:13:00
 0:10:27
0:10:27
 0:18:21
0:18:21
 0:17:29
0:17:29
 0:01:19
0:01:19
 0:19:02
0:19:02
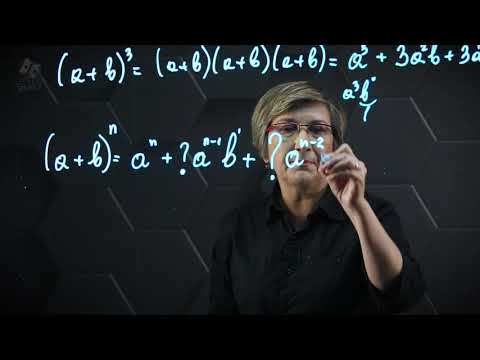 0:11:47
0:11:47
 0:17:35
0:17:35
 0:01:00
0:01:00
 0:14:40
0:14:40
 0:30:28
0:30:28
 0:14:43
0:14:43
 0:03:30
0:03:30