filmov
tv
Proof for Absolute Value of a Convergent Sequence | Real Analysis Exercises

Показать описание
We prove that if a sequence (a_n) converges to a, then (|a_n|) converges to |a|. That is, if a sequence converges to a finite limit, then the absolute value of the sequence converges to the absolute value of the limit. We prove this using the epsilon definition of the limit of a sequence and the reverse triangle inequality. #RealAnalysis
★DONATE★
Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!
Follow Wrath of Math on...
★DONATE★
Thanks to Robert Rennie, Barbara Sharrock, and Rolf Waefler for their generous support on Patreon!
Follow Wrath of Math on...
Proof: Product of Absolute Values is the Absolute Value of the Product
Proof: A Useful Absolute Value Inequality | Real Analysis
Absolute Value and Proof by Cases
Triangle Inequality for Real Numbers Proof
proofs of fundamental absolute value properties
Proof of Main Lemma for Absolute Value
Proof for Absolute Value of a Convergent Sequence | Real Analysis Exercises
Inequality Proof: Example with Absolute Value and x^2 using Cases
72. (a) Show that the absolute value function F(x)=|x| is continuous everywhere.
Reverse Triangle Inequality Absolute Value Proof
proof of absolute value inequality
How To Solve Absolute Value Equations, Basic Introduction, Algebra
Proof: Triangle Inequality Theorem | Real Analysis
Proof that the Absolute Value Function is Not Differentiable at Zero
Proof of an Absolute Value Theorem
Proof: Reverse Triangle Inequality Theorem | Real Analysis
The Absolute Value of a Product is the Product of the Absolute Values
Absolute Value Inequality Tool and its Proof | Meta4Math (ON MUTE) | Intro to Analysis
2.4 Distance and absolute values
Real Analysis Course #9 - The Absolute Value Function and Properties
Meaning of absolute value
Proof: Absolute Value Theorem for Sequences | Real Analysis
Absolute value property 1
Absolute Values - Properties and Rules
Комментарии
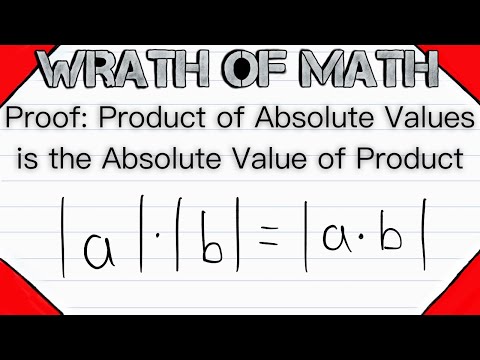 0:05:15
0:05:15
 0:07:45
0:07:45
 0:06:47
0:06:47
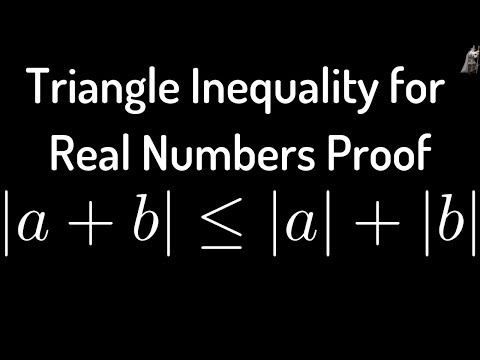 0:03:08
0:03:08
 0:13:56
0:13:56
 0:06:43
0:06:43
 0:05:45
0:05:45
 0:06:03
0:06:03
 0:06:59
0:06:59
 0:03:37
0:03:37
 0:09:49
0:09:49
 0:04:21
0:04:21
 0:05:30
0:05:30
 0:03:10
0:03:10
 0:09:49
0:09:49
 0:08:53
0:08:53
 0:05:31
0:05:31
 0:07:42
0:07:42
 0:03:31
0:03:31
 0:03:24
0:03:24
 0:03:40
0:03:40
 0:07:46
0:07:46
 0:05:11
0:05:11
 0:08:35
0:08:35