filmov
tv
Math Olympiad Question | Can You Solve This?
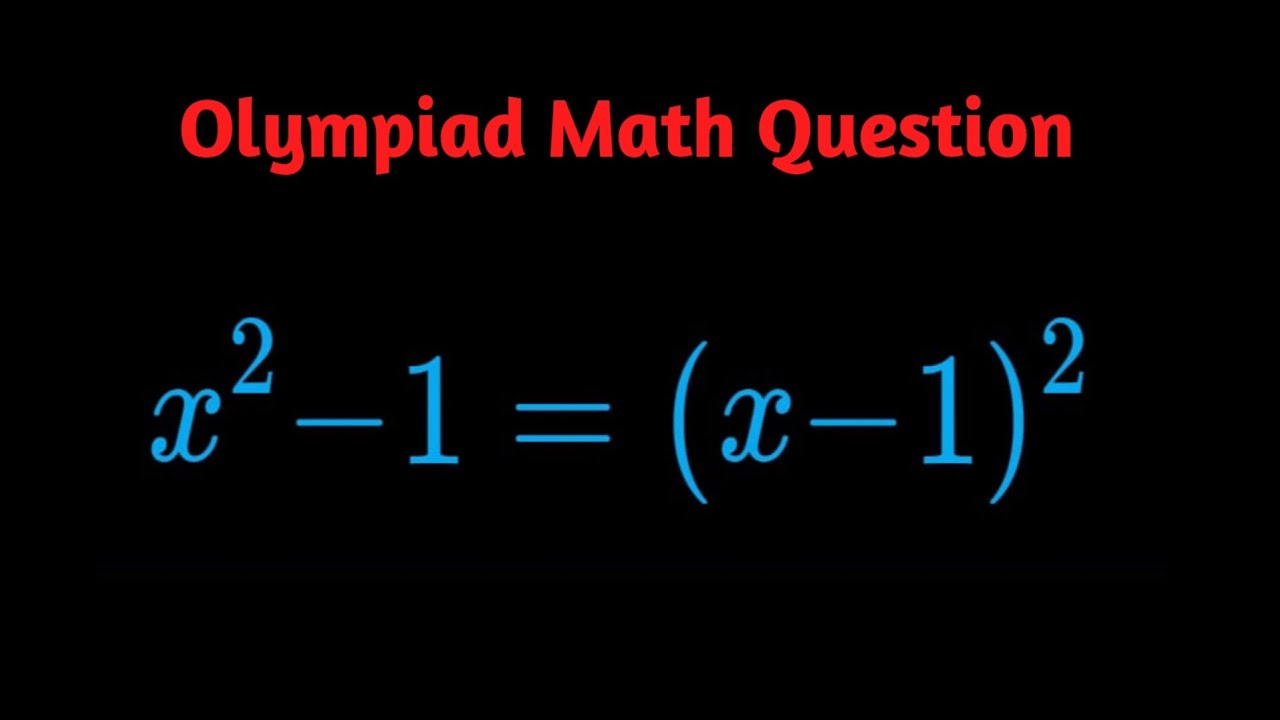
Показать описание
Hello My Dear Family😍😍😍
I hope you all are well 🤗🤗🤗
If you like this video about
How to solve this algebra equations
Math Olympiad
please Like & Subscribe my channel ,🙏🙏🙏🙏
video #trending #viralvideo #viral
#maths #algebra #matholympiad #mathematics #math #exponentialequation
Some important playlist
💭Math Olympiad Questions
Hello Everyone 🤗🤗🤗
If you like this video about
Math Olympiad and
Nice Exponential Problem - How to Solve It
please Like & Subscribe my channel ,🙏🙏🙏🙏
#matholympiad
learncommunolizer Math Olympiad Question | college level |solving Exponential Equation
@mathwindow
@PreMath
@JusticeShepard
@bprpPrecalculus
@SyberMath
Topics Covered :-
international math Olympiad
Math Olympiad Problem
Algebra Problem
Olympiad Mathematics
System of Equations
math olympiad algebra problem
math
olympiad mathematics
math olympiad preparation
mathematics
maths
math olympiad questions
math olympics
math problems
olympiad
premath
math olympiad problems
challenging math problems
algebra
sybermath
algebra 1
algebra 2
sat math
quadratic equations
algebraic equations
nice algebra problem
olympiad exam 2022
pre math
imo
math olympiad question
high school math
math olympiad
how to study math
college math
algebra problem
precalculus
math olympiad problems with solutions
challenging math questions
trending math problem
olympiad trending math questions
difficult math equations
mathematical olympiad
challenging math
trending mathematics
olympiad math
algebra for beginners
math problems with solutions
math olympiad solutions
math competition solutions
solve for x
difficult math problems
#maths #algebra #mathematics #mathematician #mathematicians #algebra #algebratricks #algebraformulas #algebrahelp #olimpiadas #olimpiadmath #algebraquestion #algebraquestions #geometry #easymaths #easymathematics #easymathematicsforyou #multiplication #division #fraction #product #laws #lawsofexponent #howtolearnmathsfromthebeginning #howtolearnmathsfrombasics #howtolearnmaths #simplemathstricks #simplemathematics #simplemath #algebrahelp #simplealgebra#relaxingmath#howtosolvepotentialequations#potentialequations#solveforx#mathssolving#exponents #equations #exponentialequation #exponentialequations #algebrahelp #algebraformulas #algebratrick #highermathematics #highermaths #highermath#programming #programmer#sinus#sinx#cosx#findthevalueof #powerdivision#ln#derivative
I hope you all are well 🤗🤗🤗
If you like this video about
How to solve this algebra equations
Math Olympiad
please Like & Subscribe my channel ,🙏🙏🙏🙏
video #trending #viralvideo #viral
#maths #algebra #matholympiad #mathematics #math #exponentialequation
Some important playlist
💭Math Olympiad Questions
Hello Everyone 🤗🤗🤗
If you like this video about
Math Olympiad and
Nice Exponential Problem - How to Solve It
please Like & Subscribe my channel ,🙏🙏🙏🙏
#matholympiad
learncommunolizer Math Olympiad Question | college level |solving Exponential Equation
@mathwindow
@PreMath
@JusticeShepard
@bprpPrecalculus
@SyberMath
Topics Covered :-
international math Olympiad
Math Olympiad Problem
Algebra Problem
Olympiad Mathematics
System of Equations
math olympiad algebra problem
math
olympiad mathematics
math olympiad preparation
mathematics
maths
math olympiad questions
math olympics
math problems
olympiad
premath
math olympiad problems
challenging math problems
algebra
sybermath
algebra 1
algebra 2
sat math
quadratic equations
algebraic equations
nice algebra problem
olympiad exam 2022
pre math
imo
math olympiad question
high school math
math olympiad
how to study math
college math
algebra problem
precalculus
math olympiad problems with solutions
challenging math questions
trending math problem
olympiad trending math questions
difficult math equations
mathematical olympiad
challenging math
trending mathematics
olympiad math
algebra for beginners
math problems with solutions
math olympiad solutions
math competition solutions
solve for x
difficult math problems
#maths #algebra #mathematics #mathematician #mathematicians #algebra #algebratricks #algebraformulas #algebrahelp #olimpiadas #olimpiadmath #algebraquestion #algebraquestions #geometry #easymaths #easymathematics #easymathematicsforyou #multiplication #division #fraction #product #laws #lawsofexponent #howtolearnmathsfromthebeginning #howtolearnmathsfrombasics #howtolearnmaths #simplemathstricks #simplemathematics #simplemath #algebrahelp #simplealgebra#relaxingmath#howtosolvepotentialequations#potentialequations#solveforx#mathssolving#exponents #equations #exponentialequation #exponentialequations #algebrahelp #algebraformulas #algebratrick #highermathematics #highermaths #highermath#programming #programmer#sinus#sinx#cosx#findthevalueof #powerdivision#ln#derivative
Комментарии
 0:03:21
0:03:21
 0:08:40
0:08:40
 0:01:54
0:01:54
 0:06:17
0:06:17
 0:08:36
0:08:36
 0:02:51
0:02:51
 0:08:01
0:08:01
 0:10:37
0:10:37
 0:01:00
0:01:00
 0:10:06
0:10:06
 0:02:34
0:02:34
 0:10:51
0:10:51
 0:10:49
0:10:49
 0:02:24
0:02:24
 0:12:35
0:12:35
 0:06:40
0:06:40
 0:56:01
0:56:01
 0:09:54
0:09:54
 0:01:12
0:01:12
 0:06:45
0:06:45
 0:08:03
0:08:03
 0:01:26
0:01:26
 0:07:35
0:07:35
 0:11:06
0:11:06