filmov
tv
One of the HARDEST International Math Olympiad Question

Показать описание
If you're reading this ❤️
A great exponential equation! What do you think about this problem?
Hello My Friend ! Welcome to my channel. I really appreciate it! Learn Mathematics with me. Have a Great Day:)
@higher_mathematics
#maths #algebra
A great exponential equation! What do you think about this problem?
Hello My Friend ! Welcome to my channel. I really appreciate it! Learn Mathematics with me. Have a Great Day:)
@higher_mathematics
#maths #algebra
One of the HARDEST International Math Olympiad Question
One of The Hardest International Maths Olympiad Problem
One of the hardest International Olympiad Math || X=?
The unexpectedly hard windmill question (2011 IMO, Q2)
The Most BRUTAL Sport In The World | Rugby's Hardest Hits, Biggest Tackles & Crazy Skills
The hardest problem on the hardest test
The hardest KO at M-1 Medieval!
One of the 'HARDEST' International Maths Olympiad Problem.
The World’s Hardest Math Class
One of The Hardest International Maths Olympiad Problems || X =?
Is this the Hardest Sound in Any Language? [Long Short]
this is the hardest guitar solo ever
Simone’s face of disappointment after landing the hardest vault in the world 😭 #olympics #gymnast...
Exponential Equation Problem from one of the Hardest International Math Olympiads || X=?
One of The Hardest International Maths Olympiad Problem
One of the 'HARDEST' International Maths Olympiad Problem.
One of the Hardest International Maths Olympiad Problem.
I visited the world's hardest math class
One of the 'HARDEST' International Maths Olympiad Problem.
The Hardest Math Test
Top 10 Hardest A-Levels #shorts #gcse #alevels #students
One of the hardest question in international math competition
The Hardest Volleyball Training!
What's the hardest piano piece? (TW: blood)
Комментарии
 0:10:51
0:10:51
 0:10:07
0:10:07
 0:06:29
0:06:29
 0:16:03
0:16:03
 0:08:24
0:08:24
 0:11:15
0:11:15
 0:01:34
0:01:34
 0:05:42
0:05:42
 0:00:34
0:00:34
 0:11:15
0:11:15
 0:01:38
0:01:38
 0:00:13
0:00:13
 0:00:08
0:00:08
 0:09:50
0:09:50
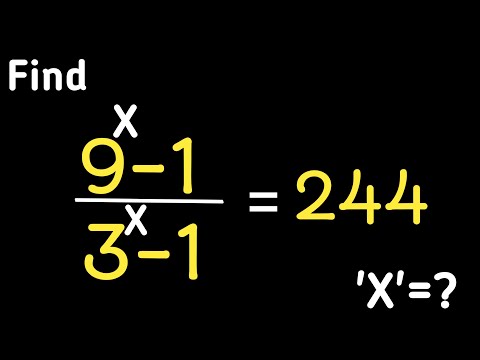 0:03:39
0:03:39
 0:02:21
0:02:21
 0:02:03
0:02:03
 0:12:50
0:12:50
 0:03:07
0:03:07
 0:00:28
0:00:28
 0:00:07
0:00:07
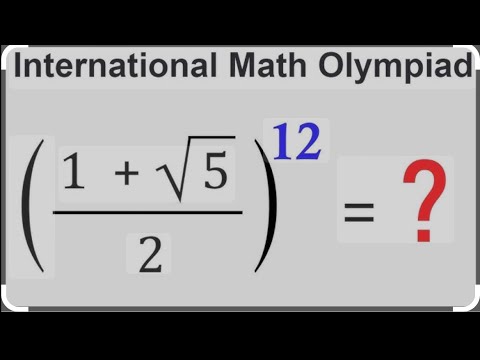 0:07:08
0:07:08
 0:00:44
0:00:44
 0:00:25
0:00:25