filmov
tv
Germany - Math Olympiad Question | The BEST Trick

Показать описание
You should know this approach. Solution
What do you think about this problem? Don't forget to like and subscribe to my channel for more helpful math tricks. Thanks For Watching!
If you're reading this ❤️. Thank You!
Hello My Friend ! Welcome to my channel. I really appreciate it!
@higher_mathematics
#maths #math
What do you think about this problem? Don't forget to like and subscribe to my channel for more helpful math tricks. Thanks For Watching!
If you're reading this ❤️. Thank You!
Hello My Friend ! Welcome to my channel. I really appreciate it!
@higher_mathematics
#maths #math
Germany Math Olympiad Question | You should know this trick!
Germany - Math Olympiad Problem | Be Careful!
Germany | Maths Olympiad Questions Solve | Find The Value of (X,Y)=?
Germany - Math Olympiad Question | The BEST Trick
Germany - Math Olympiad Question -
Germany | Can you solve this ? | Math Olympiad Radical Simplification | You Should Know this trick
Germany | Math Olympiad Question | You should be able to solve this!
Germany -Math Olympiad question|Solve for x and y#math #matholympiad
German math Olympiad. A nice trick used in solving Olympiad math problem on exponential equation.
Germany Math Olympiad Question | Geometry | Find X
Germany Math Olympiad Problem | Best Math Olympiad Problem | Geometry
Germany | A Tricky Maths Olympiad Question | Square Roots |
Germany |A nice Math Olympiad Problem | Ca you sove this x=? & y=?
Germany Math Olympiad, a system of cubic equations
Germany Math Olympiad Question | Algebra Problem for Geniuses
Germany | Exponential equation solving | Math olympiad equation
Germany - Math Olympiad Question | Best Trick!!!
Germany Math Olympiad Question || How To Solve For x? || Can You Solve It?
Luxembourg - Math Olympiad Question | You should know this trick
Japanese| A nice math Olympiad question #maths #matheolympiad
Germany - Math Olympiad Exponential Problem @Mamtamaam
Germany - Math Olympiad Exponential Problem.
German Maths Olympiad Question.With Trick best solution
German - Math Olympiad Question. Exponent Problem.
Комментарии
 0:11:10
0:11:10
 0:10:06
0:10:06
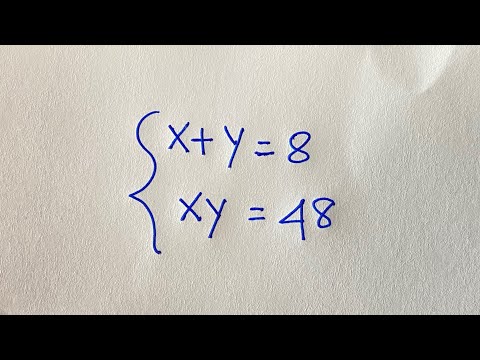 0:08:52
0:08:52
 0:10:37
0:10:37
 0:03:19
0:03:19
 0:10:33
0:10:33
 0:01:54
0:01:54
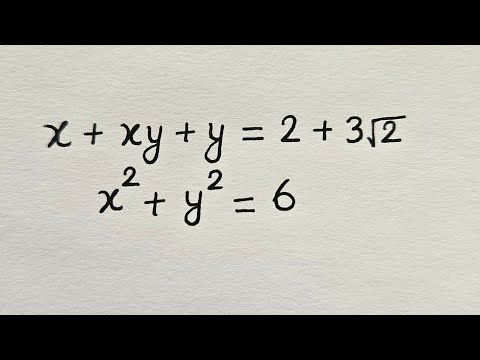 0:11:52
0:11:52
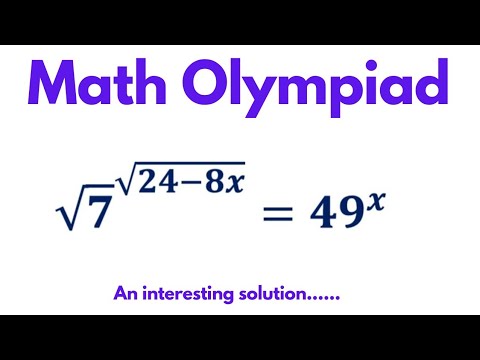 0:07:12
0:07:12
 0:12:52
0:12:52
 0:14:56
0:14:56
 0:08:35
0:08:35
 0:12:53
0:12:53
 0:11:36
0:11:36
 0:06:38
0:06:38
 0:11:43
0:11:43
 0:02:14
0:02:14
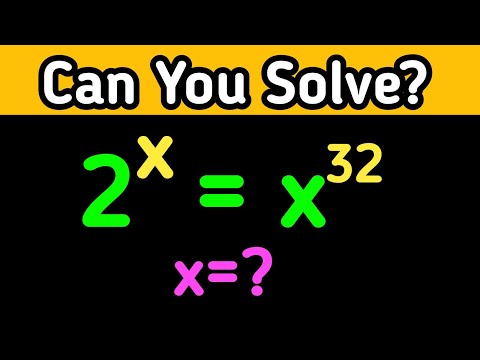 0:06:41
0:06:41
 0:02:51
0:02:51
 0:09:55
0:09:55
 0:08:04
0:08:04
 0:04:45
0:04:45
 0:07:00
0:07:00
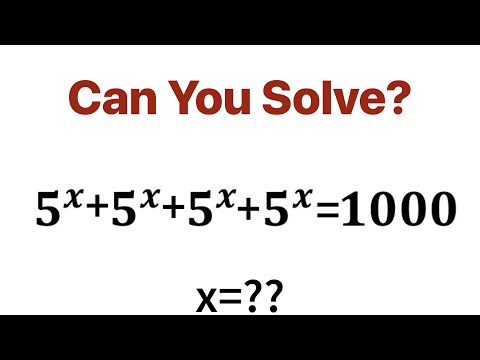 0:03:11
0:03:11