filmov
tv
I Solved A Nice Polynomial System

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#polynomials #polynomialequations #algebra
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#polynomials #polynomialequations #algebra
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
I Solved A Nice Polynomial System
I Solved A Nice Polynomial Equation in Two Ways
Solving a Nice Polynomial System in Two Ways
Solving a Nice Polynomial Equation
Solving a Nice Polynomial System in Two Ways
Solving a Nice Polynomial System in Two Ways
Solving A Nice Polynomial System | Algebra
A Nice Polynomial Equation | Algebra
Solving A Nice Polynomial Equation
A Nice Polynomial Equation from Croatia 🇭🇷
A Nice Polynomial Equation
A Nice Polynomial System
Solving A Nice Polynomial Equation
A nice polynomial problem with primes.
A Nice Polynomial System
Solving A Nice Polynomial System | Two Ways
Solving A Nice Polynomial System by Math26039335
Solving Polynomial Equations By Factoring and Using Synthetic Division
Let's Solve A Nice Polynomial System
Solving an Undecic Polynomial Equation
a nice integer polynomial equation
Let's Solve A Nice Polynomial Equation | Math Olympiads
A Nice Polynomial System | #algebra #polynomials
Let's Solve A Nice Polynomial Equation | Math Olympiads
Комментарии
 0:06:23
0:06:23
 0:10:45
0:10:45
 0:08:38
0:08:38
 0:05:53
0:05:53
 0:09:27
0:09:27
 0:09:03
0:09:03
 0:08:57
0:08:57
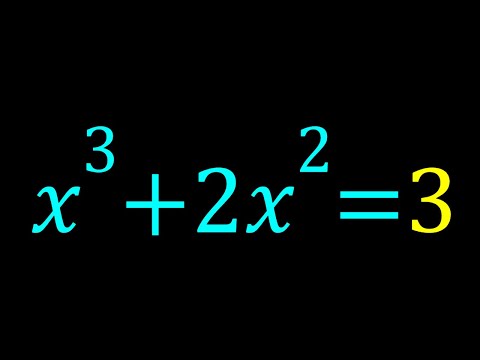 0:10:00
0:10:00
 0:08:35
0:08:35
 0:09:27
0:09:27
 0:00:51
0:00:51
 0:08:40
0:08:40
 0:08:20
0:08:20
 0:01:00
0:01:00
 0:08:19
0:08:19
 0:10:56
0:10:56
 0:11:06
0:11:06
 0:14:19
0:14:19
 0:10:27
0:10:27
 0:17:54
0:17:54
 0:14:18
0:14:18
 0:10:49
0:10:49
 0:08:16
0:08:16
 0:09:34
0:09:34