filmov
tv
Let's Solve A Nice Polynomial Equation | Math Olympiads
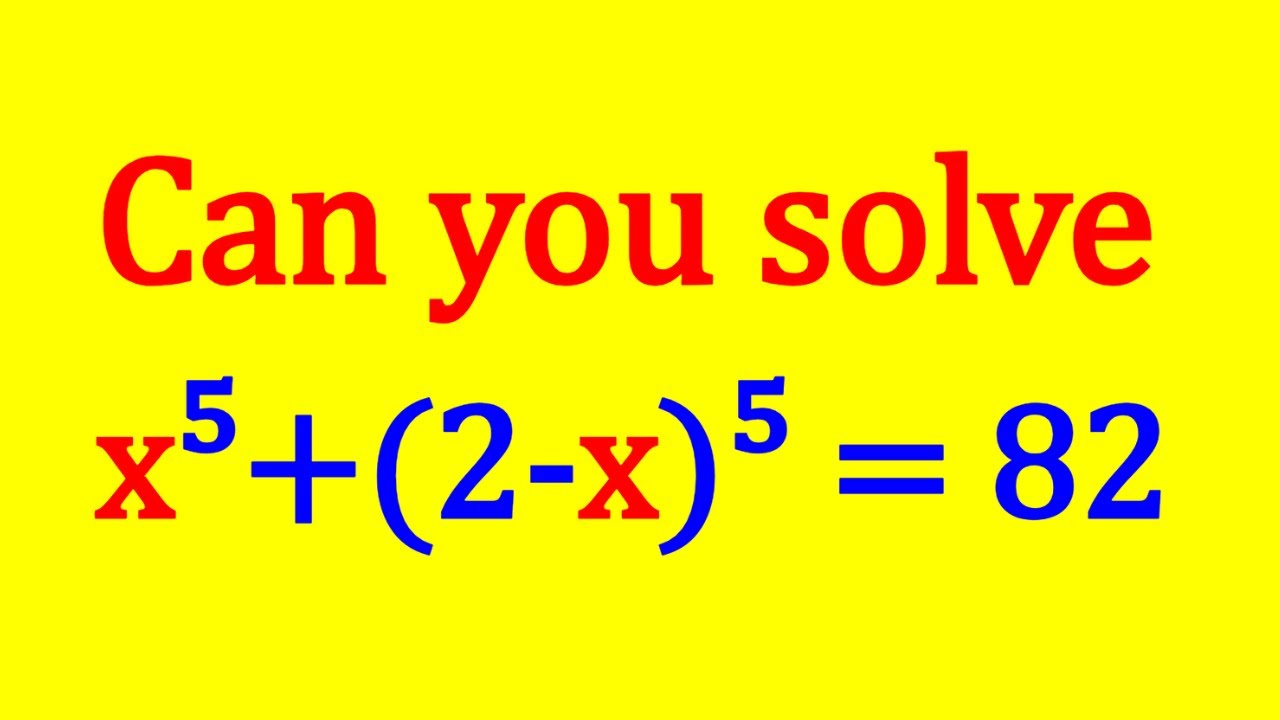
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries #sequence
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries #sequence
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Let's Solve A Nice Polynomial Equation | Math Olympiads
Let's Solve A Nice Polynomial System
A Nice Polynomial System
Let's Solve A Nice Polynomial Equation | Math Olympiads
A Nice Polynomial Equation | Algebra
Solving a Nice Polynomial Equation
Solving a Nice Polynomial System in Two Ways
Solving a Nice Polynomial System in Two Ways
A Nice math Olympiad exponential question|can you solve for x|math Olympiad.
A Nice Polynomial System
Solving A Nice Polynomial Equation
Solving a Nice Polynomial System in Two Ways
I Solved A Nice Polynomial System
✅ FACTORIZATION of a POLYNOMIAL, polynomials 🎓 #polynomials #maths #shorts
A Nice Polynomial Equation from Croatia 🇭🇷
Solving A Nice Polynomial Equation
Evaluating Polynomial Expressions | Math Olympiads
A Nice Polynomial System
An Interesting Polynomial System
A Cool Polynomial System | Nice Graph!
Unique SAT Polynomial Question that is not Hard at all
A Nice Polynomial System | Math Olympiads
A Very Nice Polynomial System
A Nice Polynomial Equation | Math Olympiads
Комментарии
 0:10:49
0:10:49
 0:10:27
0:10:27
 0:08:40
0:08:40
 0:09:34
0:09:34
 0:10:00
0:10:00
 0:05:53
0:05:53
 0:09:27
0:09:27
 0:08:38
0:08:38
 0:07:04
0:07:04
 0:08:19
0:08:19
 0:08:35
0:08:35
 0:09:03
0:09:03
 0:06:23
0:06:23
 0:00:19
0:00:19
 0:09:27
0:09:27
 0:08:20
0:08:20
 0:00:56
0:00:56
 0:08:13
0:08:13
 0:09:58
0:09:58
 0:11:19
0:11:19
 0:00:59
0:00:59
 0:00:37
0:00:37
 0:10:31
0:10:31
 0:09:32
0:09:32