filmov
tv
A Cool Functional Equation
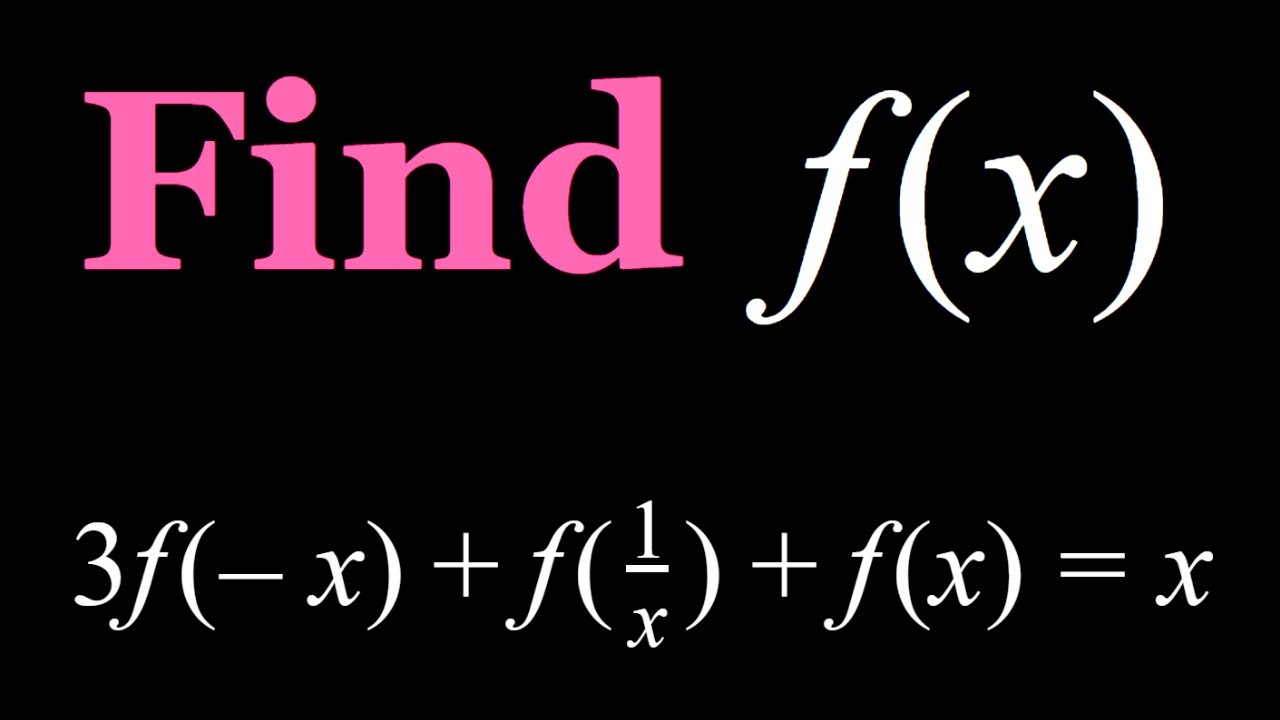
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
A Cool Functional Equation
A Cool Functional Equation
A Cool Functional Equation
the greatest functional equation of all time.
a fun functional equation
A Cool Functional Equation
Solving a Rational Functional Equation | Find f(x) |A Cool Functional Equation
One of the coolest functional equations I have seen!
A Curious Functional Equation | Math Olympiads
Some Cool Functional Equations
International Math Olympiad Shortlist 2015 Problem A2 - A cool functional equation on the integers
A Nice and Easy Functional Equation
My functional equation, is it cool?
I Solved A Cool Functional Equation
Cool Functional Equation
A nice functional equation from Romania
Solving A Functional Equation
A fun functional equation!!
A functional equation from my favorite book.
A Functional Equation with Golden Flavor
Solving a Quick and Easy Functional Equation
A Functional Equation from Samara Math Olympiads
A functional equation from @goodplacetostop2973
A functional equation from Kyrgyzstan
Комментарии
 0:12:43
0:12:43
 0:05:38
0:05:38
 0:09:13
0:09:13
 0:07:48
0:07:48
 0:09:20
0:09:20
 0:05:15
0:05:15
 0:04:08
0:04:08
 0:15:34
0:15:34
 0:08:29
0:08:29
 0:16:59
0:16:59
 0:17:05
0:17:05
 0:05:07
0:05:07
 0:02:39
0:02:39
 0:06:01
0:06:01
 0:00:45
0:00:45
 0:18:36
0:18:36
 0:00:29
0:00:29
 0:11:13
0:11:13
 0:11:23
0:11:23
 0:07:21
0:07:21
 0:08:18
0:08:18
 0:08:47
0:08:47
 0:08:18
0:08:18
 0:12:02
0:12:02