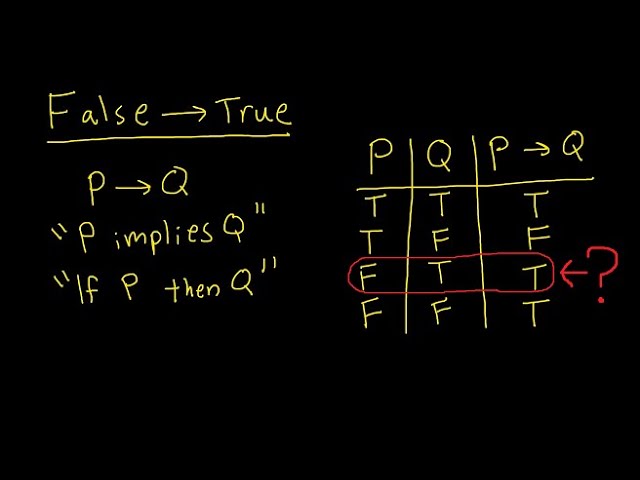
Why does 'False imply True' in logic?

[High School Level] - In this video I discuss something in symbolic logic that always bothered me: why does "false" imply "true"? I look at the question from a variety of perspectives in order to get an answer.

[oliver]

After a while of thinking about it, the way I understood "F -> T = T" it is that P -> Q translates to "P is one of the circumstances in which Q can be true, but Q can be true without P nessecarily being true".

Eg. Using one of the examples in the video, "If I wake up at 9 am I will be late to school". You can be late to school for many different reasons, waking up at 9 am can be one of them, but there are other reasons you can be late to school. Extending this to "T -> F = F", if you wake up at 9 am, there is no possible way you will not be late to school, therefore it can never be false that you are late to school.

[GustavoOliveira-gpnr]

I think a little different from these answers you gave in the video.

F -> T is just a convention in the end of the day, just like 1 + 0 = 1. You could build a completly new mathematical field by postulating "1 + 2 = 8". Hyperbolic geometry was born by postulating weird assumptions about geometry, but it is true and genuine math nonetheless.

The problem comes when you mix the mathematical sentence with intuitions about english language.

In the same way, i could wonder "why T or T = T?". Because in the english language, we ususally use the word "or" as exclusive, not inclusive. Consider this sentence:
"My car is blue OR i have a duck"
From a mathematical perspective, the car being blue and having a duck can both be true making the whole sentence true, but a mathematical iliterate person my be confused by this proposition, he might ponder "when someone says OR, he means 1 of the 2 options is correct, it can't be both, it is either one or the other!"
In his mind, given that A and B are both true, to say "A or B is true" sounds weird, because the word OR is usually taken the have an exclusive meaning in daily language.
Here you can see the intuition behind language causing confusion with intuition of mathematical sentences.

The problem comes from the fact that mathematical language formalism is not necessarily coherent and correspondent with daily language. They are usually similar, but not necessarily equal in meaning.

Therefore, it has been conventioned that AND has the truth table it has, and OR has the truth table it has, although we could have built set theory with other arbitrary operations with different truth tables given that they were linearly independent. It is just that these choices of operations have easy intuitions that resemble our own language, thus these choices.

For instance, (P -> Q) is formally defined to be (~P v Q), the "->" symbol is just and abreviation.


Also, the reasoning behind causality is important too. It is important to note that causality pressuposes the notion of 'time', any cause must precede an effect in time.

But mathematics has not time in it. When I have a function like
f(x) = 5x,
and then I input x=2 making
f(2) = 10,
It is not that "x=2 CAUSED f(x) to become 10", it just is. Mathematical truths are analytic, there is no notion of causality in mathematics. Physichs has causality in its intuitions and reasoning, Math has not.

Pure math is not about time, it is exactly the opposite, Math is about eternal immutable truths, that is why causality is not a topic related to pure math.

[vladislavanikin]

A mathematically illiterate math student here with some perspective that helped me find peace with F→T being a true statement. it's a long and probably wrong comment, so you would be better by skipping it. The comment:

There are two points to consider.

Point #1. First of all, I think Naomi is right in that P→Q is not a statement on causality, but I wouldn't say it's a statement of a fact. It's just a statement. What kind of statement? The same kind as P^Q (that's an "and"). We wouldn't force P and Q be causally connected, hell, we wouldn't force P and Q be connected at all to evaluate the truth value of P^Q, so for what reason do we try to do it with P→Q? It's because of the name. Implication. We think about this type of statements differently, we feel them differently, however, in formal logic they are the same type of statements. They have to be, because formal logic doesn't concern itself with meanings of individual statements, only with forms of their compositions, hence the name "formal". So one can say that all the confusion is an artifact of our thinking and our desire to have a connection between P→Q and our language, even though it being a connective from formal logic we should have a way to evaluate truth values of « *If* I am a giant squid, *then* the Moon is made out of cheese ».
But why call it "if, then" statement then? That's my...

Point #2. Think not about when P→Q is true, but when it is definitely false. Or better yet when would it be the case if someone said to you "If P then Q" you would think they lied. No matter the content. For example, if someone said to a child of theirs something like "If you get an A mark on the test, I will buy you an ice cream" when they would be lying? Clearly they would be lying if the child gets an A and they doesn't buy an ice cream, but if a child doesn't get an A and they still buys one that wouldn't be a lie (I think most children wouldn't accuse their parent in this situation). That makes P→Q (given that the parent's statement is indeed a P→Q statement) true even in the case of false antecedent and true consequent, and it's easy to see that it's a matter of the form and not the content (hopefully that's easy to see). Therefore, I would argue, it's better to think about truth table for implication not in terms of "when it's true", but rather "when it's false".

In conclusion, I think that F→T and the ability to connect via implication two completely different statements are in fact two different problems. The first one is excellently explained by Theo and the second one has to do with a clash between "formal" part in formal logic and our general use of "if, then" connective as an expression of causality or a fact or something else entirely, when in logic it's a statement just as «I am a giant squid *and* the Moon is made out of cheese». (I just have to have a silly joke at the end...)

[AD]

This video needs more of a discussion regarding vacuous truths; It seems to imply that implication does not lead to vacuous truths in pure mathematics. Wikipedia has a great example with inequalities:
For any integer x, "if x > 5 then x > 3." So, P = x>5 and Q =x>3..

Think of the case when x=4..

[sonpa]

So it would seem it's more so correlation rather than causation and that all that matters is the outcome. It would only seem causation for "if and only if".

[mescwb]

Gustavo Oliveira in these comments said it alll. "P->Q" is a MERE ABREVIATION of "(~P v Q)". Simplicity to write at the cost of eventual confusion if paired to day 2 dayy language. Hence it's "independent of English" and easy to get it when reminding is an abreviation for fundamental operators expression - like x to +, a sucession of sums of a same number - hey, "x to +" ≈ "P->Q is to (~PvQ) 🙂

[pyropulseIXXI]

The only reason is because it is literally defined that way. There is no reason beyond that. If P is false, then you cannot infer anything about Q. You should've asked "why does false imply false?" To the naive, this seems obvious, but it isn't, because if P is false, then you cannot infer anything about Q, so if Q is true is the same as if Q is false.

For instance, if 1 > 5, then 1 > 3 is TRUE, and that is a case of "false implies false."

[Arson_Oakwood]

I struggled with it because of poorly written example in my native language book of logic, which stated that "If weather will be good, we will go to the forest", checking conditions under circumstance "in which situation the promise was fulfilled", stating that even if weather is bad, but we are in the forest, promise was held. My language is made the way, that if we state condition, it necessitates result, and if condition is not met, there couldn't be result, meaning, if weather is bad, you wouldn't go in the forest in the first place to make the statement true, so it was like, how it is possible that Q is true, if we stated that Q is true when P is true. Then I understood that language is structured in form of "if and only", and we shouldn't question "in which situation the promise was fulfilled", but rather "In which cases we are content with getting what we were promised with", like if I want to go to forest no matter what, I don't have problem with bad weather. So there is difficulty in interpreting imply through common speech.

[mikiyasalemu]

The best explanation that I have is interms of universal quantified statements ( kind of similar to theo's answer ). Now for example If I say
" For all x, If x is human then x is mortal" this statement must be true in intuitive matter. And we know that this statement is true if the sentence "If x is human, then x is mortal" is true for all x.( now when we say "all x" is that x could be absolutely anything, maybe car or an idea or a number ). And the statement is false is there is one x, such that the sentence " If x is human, then x is mortal " is false. Now here is the main takeaway, suppose x is a cat. Now according to our statement the statement "If a cat is human, then a cat is mortal" must be true( since the the universal quantified statement is true ) but the sentence "a cat is human" is false and "a cat is mortal" is true. Now if we let "p implies q" to be false when p is false and q is true, then the sentence "If a cat is human, then a cat is mortal" is false. Hence I have found one x ( a cat ) such that the statement is false. Hence the universal quantified statement is false. But this contradicts the fact that the the statement was true( atleast intuitively ). And to avoid this contradiction, "p implies q" is true when p is false and q is true. Now you might say that why must the truth value of "p implies q" is changed for the sake of universal quantified statements. You might not believe it but the universal quantified statement is almost in every theorem, particularly the universal quantified conditional statements ( like the example I gave ). For example the pythagorean theorem is a universal quantified conditional statement.
For all x, if x is a right triangle and a and b are the lengths of the legs of the triangle and c is the length of the hypotenuse, then a^2 +b^2 = c^2.
I hope this helps:)

[saityusufbulur]

The logical statement "A implies B" expresses the "If A is true, B is also true" connection between A and B.

Notice that it doesn't refer to A or it doesn't refer to B, but to the CONNECTION between A and B. So to make the statement "A implies B" false you must break this "If A is true, B is also true" connection. There is only one way to break this connection. A will be true, but B will be false independently of A. Thus, the connection between the two will be broken and the truth value of the statement "A implies B" will be false.

[DDvargas]

the concept of the phrase "when pigs fly" is how i think about it
"if [impossible thing happens] then [anything could happen]"

[tanyongkang]

From my understanding, there are 2 conditions

Q must be inherently right or wrong, P isn't the only factor to determine the outcome of Q.

Idk HAHA

[TwoForFlinchin]

So it seems like "implication" has more to do with whether two things can possibly be true at the same time and not whether the truth of one proposition is necessarily tied to the truth of another.

[jacoboribilik]

To me p implies q is simply a propositional logic function that takes truth values and spits out other truth values. It's just a convenient way of stating mathematical theeorems. Just like conjunctions or disjunctions. When you come across a math theorem claiming "p then q" is true then you should take it as a simple, formal, succint, lacconic way of telling you "in case p is true you'll also have q true and in case p is not true then I don't know which value q might take on". In a way, one is solving for the value of q: I tell you p->q=1 then you know p=1 yields q=1. All the semantics and philosophical garble that mudy the waters are simlply outside the realm of mathematics and much confusion could have been spared if propositional logic functions were seen in that fashion.

[Mr_Bryan]

Just for the fun: the Greek word that Aristotle would have used for category is κατηγορία (‘categoria’) — Latin used the same word, too.

[Bozeman]

P=>Q is true where P is false because it does not comment on worlds in which P is false, and thus cannot be contradicted by them.

[MrRyanroberson]

TL;DR: "implies" is a misnomer that leads to confusion. All logic would be completely unchanged if we just replaced "P implies Q" with "Q or not P"
that's it, it's another logical operation like "and", "or", and "xor". There's also the version of "-", "P and not Q" which has its own uses.

[chrihipp]

Namoni's reasoning gets the point IMO, but the expalnation was 😵‍💫.
It's maybe easier, if the focus in on Q and not on P. In the sense that P is a possible cause for Q.
2 points should be clear: [1] Q is a fact, [2] It's not in question that P is a cause for Q.

P => Q : TRUE per definition
P => ¬Q : FALSE per definition
¬P => Q : TRUE b/c Q is a fact and there is a valid cause ¬P
¬P => ¬Q : TRUE b/c virtually anything fulfills ¬P for ¬Q


Example 1 - P: "It did rain" Q: "The street is wet"

P => Q : TRUE b/c the street is be wet and it rained
P => ¬Q : FALSE b/c the street is not wet and it rained
¬P => Q : TRUE b/c the street is wet for some other reason than rain
¬P => ¬Q : TRUE b/c the street is not wet and monday is a weekday


Example 2 - P: f(x)=x*x Q: f(2)=4

P => Q : TRUE b/c f(2)=4 and f(2) is 2*2 is 4
P => ¬Q : FALSE b/c f(2)!=4 and f(2) is 2*2 is 4
¬P => Q : TRUE b/c f(2)=4 and 5-1=4
¬P => ¬Q : TRUE b/c f(2)!=4 and whatever

[stefanobarbotto]

9:47 But, to be sure your sentence is true, you would have to know when P-->Q is true, since it is an if clause, right? So, if I'm not mistaken this would invalidate the argument

[rishabhnarula]

We say that an implication p --> q is vaccuously true if p is false. Since now it's impossible to have p true and q false. That is we can't check anymore whether the contrary, p being true and q being false, can be.Since p being true is non-existent. So we take the implication as true. For eg. If 3 squared = 27, then 2+2=5. Can we check if it is indeed true that 3 squared equals 27 then 2+2 is not 5. No. Because 3 squared equals 27 is non-existent. Or false. So we can't check if the statement is false. Hence it must be true.vaccuously.