filmov
tv
How to Solve Logarithmic and Exponential Equations with Different Bases: Step-by-Step Tutorial

Показать описание
Logarithms - The Easy Way!
Solving Logarithmic Equations
Solving Exponential and Logarithmic Equations
Logs Everything You Need to Know
solving a logarithmic equation with different bases
Solving Logarithmic Equations... How? (NancyPi)
Solving logarithmic equations | Exponential and logarithmic functions | Algebra II | Khan Academy
SOLVING LOGARITHMIC EQUATIONS || FINDING THE VALUE OF X
Solving Logarithmic Equations | Algebra Two | 11th Grade
Solving logarithmic equations by factoring
Logarithmic equation
Lesson 3 Logarithms, Solving Logarithmic and Exponential Equations
Solving Logarithmic Equations (5 Examples)
How to Solve Logarithmic and Exponential Equations with Different Bases: Step-by-Step Tutorial
Properties of Logarithms
Rules of Logarithms | Don't Memorise
solving a logarithmic equation with different bases
04 - Solving Logarithmic Equations - Part 1 - Equations with Log(x)
How to Solve Logarithmic Equations with Three Different Bases: Step-by-Step Explanation
Logarithmic Equations
Logarithmic Equations
Solving an logarithmic equation
Solving Exponential and Logarithmic Equations (Multiple Examples)
how to solve logarithmic equations with different bases
Комментарии
 0:10:20
0:10:20
 0:25:27
0:25:27
 0:07:08
0:07:08
 0:20:27
0:20:27
 0:06:02
0:06:02
 0:15:05
0:15:05
 0:04:13
0:04:13
 0:14:27
0:14:27
 0:17:24
0:17:24
 0:07:00
0:07:00
 0:03:27
0:03:27
 0:16:33
0:16:33
 0:11:04
0:11:04
 0:08:17
0:08:17
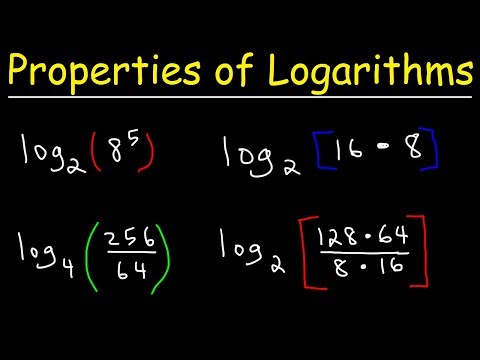 0:05:40
0:05:40
 0:04:31
0:04:31
 0:04:10
0:04:10
 0:27:26
0:27:26
 0:09:12
0:09:12
 0:09:13
0:09:13
 0:12:59
0:12:59
 0:06:41
0:06:41
 0:12:27
0:12:27
 0:05:10
0:05:10