Prove that Every Group Homorphism Maps the Identity Element to the Identity Element

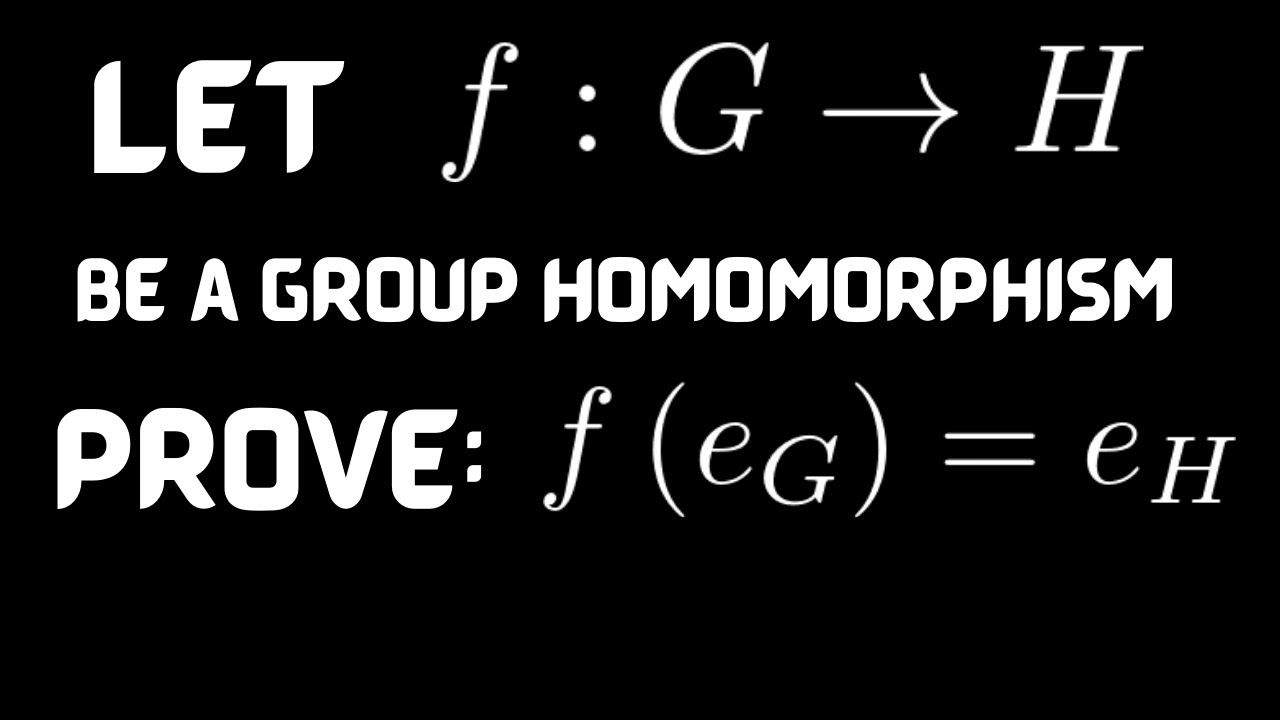
Показать описание

Prove that Every Group Homorphism Maps the Identity Element to the Identity Element

If you enjoyed this video please consider liking, sharing, and subscribing.

There are several ways that you can help support my channel:)

************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course

Advanced Calculus Course

Calculus 1 Course

Calculus 2 Course

Calculus 3 Course

Calculus Integration Insanity

Differential Equations Course

College Algebra Course

How to Write Proofs with Sets Course

How to Write Proofs with Functions Course

Statistics with StatCrunch Course

Math Graduate Programs, Applying, Advice, Motivation

Daily Devotionals for Motivation with The Math Sorcerer

Thank you:)

Рекомендации по теме

Комментарии

So because f(xy) on the left is the binary operation in group G and f(x)f(y) on the right is the binary operation in group H, I sometimes use SQUARE for the binary operation in G and TRIANGLE for the binary operation in H. I think things would be more clear for people if you made it explicit, instead of "overloading" the multiplication operator people are familiar with in regular algebra. So I would have f (x SQUARE y) = f(x) TRIANGLE f(y).

MrCoreyTexas

Please say using the associative axiom of the group theory in the process of the right hand side's change.

shunsukenatsusawa

What subject is this from, complex analysis?

SequinBrain

Prove that Every Group Homorphism Maps the Identity Element to the Identity Element

Prove that Every Group Homorphism Maps the Identity Element to the Identity Element

Group Homomorphisms - Abstract Algebra

The Kernel of a Group Homomorphism – Abstract Algebra

Group Homomorphism and Isomorphism

Group Homomorphism Proof (Example with e^x)

Normal Subgroups and Quotient Groups (aka Factor Groups) - Abstract Algebra

Proving a Function is a Group Homomorphism (Example with the Modulos)

Fundamental Theorem of Group Homomorphism

Prove that f(x^(-1)) = f(x)^(-1) for a Group Homomorphism

Definition of a Group Homomorphism and Sample Proof

Homomorphisms (Abstract Algebra)

The Image of a Group Homomorphism is a Subgroup (Proof)

Chapter 6: Homomorphism and (first) isomorphism theorem | Essence of Group Theory

Isomorphisms (Abstract Algebra)

A Group Homomorphism is Injective iff it's Kernel is Trivial Proof

Abstract Algebra | First Isomorphism Theorem for Groups

Isomorphic Groups and Isomorphisms in Group Theory | Abstract Algebra

HOMOMORPHISM PRESERVES IDENTITY AND INVERSE | DISCRETE MATHEMATICS| UNIT-4| VIDEO-16

Fundamental theorem of homomorphism of group .

11. Homomorphism of groups || Examples || Epimorphism, Monomorphism, Isomorphism || Group theory

Every Group of Order Five or Smaller is Abelian Proof

Kernel of a Group Homomorphism is a Subgroup Proof

Group Theory | Homomorphism | Fundamental Theorem Of Homomorphism | Proof

Group Homomorphisms Map the Identity to the Identity (Proof)