filmov
tv
Prove that f(x^(-1)) = f(x)^(-1) for a Group Homomorphism

Показать описание
We are given a group homomorphism from a group G into a group H. We show that f(x^(-1)) = f(x)^(-1). I hope this helps someone learning abstract algebra.
(these are my affiliate links)
***********Math, Physics, and Computer Science Books***********
These are my affiliate links. As an Amazon Associate I earn from qualifying purchases.
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
(these are my affiliate links)
***********Math, Physics, and Computer Science Books***********
These are my affiliate links. As an Amazon Associate I earn from qualifying purchases.
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
Proof that f(x) = 1/x is not Uniformly Continuous on (0,1)
Proof that f(x) = 1/x is Continuous on (0, infinity) using Delta-Epsilon
If f(x +1/x) = x - 1/x , find f(x)
How to Prove the Rational Function f(x) = 1/(x - 2) is Surjective(Onto) using the Definition
Finding the Derivative of an Inverse Function - Calculus I
function f(x)=1 , x is rational ∧ f(x)=0 , x is irrational is not Integrable on [0,1] ,Real Analysis...
Proof that f(x) = x^2 is Uniformly Continuous on (0, 1)
5 simple unsolvable equations
If , find b Check to see that your answer to part a is reasonable by comparing the graphs of and
Proof: f(x) = |x| is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Prove that the function f(x) = 1/x^2 is uniformly continous on [a, infinity)
[Proof] Function is bijective
How REAL Men Integrate Functions
If `f(x)=log((1-x)/(1+x)),` show that, `f(x)+f(y)=f((x+y)/(1-x y))`
3.5 Video #2 prove f(x) = 1/x is not uniformly Continuous
Show that f(x) is continuous at x=4
How to Prove a Function is Injective(one-to-one) Using the Definition
This is a very famous limit
#07 prove that f(x)=1/x^2 is uniform contiouous on [a ,infinite) but not UC on (0, infinite)
Finding the inverse of a function
Proof: f(x) = x is Continuous using Epsilon Delta Definition | Real Analysis Exercises
f(x) = 1/x is not uniformly continuous on (0,1)|Examples of not uniform continuity |Real Analysis
How to show that a Function is One-to-One algebraically | SHS 1 ELECTIVE MATH
How To Find The Inverse of a Function
Комментарии
 0:04:40
0:04:40
 0:09:56
0:09:56
 0:05:58
0:05:58
 0:06:03
0:06:03
 0:05:33
0:05:33
 0:07:07
0:07:07
 0:03:34
0:03:34
 0:00:50
0:00:50
 0:05:20
0:05:20
 0:04:19
0:04:19
 0:13:57
0:13:57
![[Proof] Function is](https://i.ytimg.com/vi/oTub-N4uopw/hqdefault.jpg) 0:08:50
0:08:50
 0:00:35
0:00:35
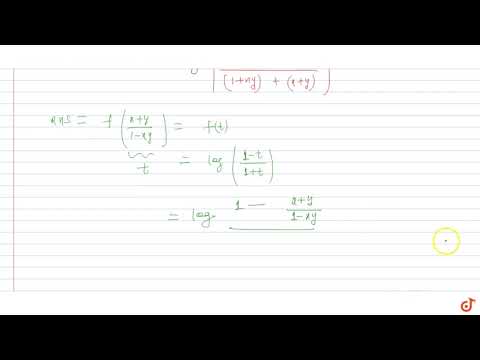 0:06:24
0:06:24
 0:17:10
0:17:10
 0:01:51
0:01:51
 0:03:35
0:03:35
 0:00:48
0:00:48
 0:14:56
0:14:56
 0:03:27
0:03:27
 0:04:46
0:04:46
 0:06:39
0:06:39
 0:10:33
0:10:33
 0:11:36
0:11:36