filmov
tv
Group Homomorphisms Map the Identity to the Identity (Proof)

Показать описание
Let G and H be groups and consider a group homomorphism from G into H. We show that f maps the identity in G to the identity in H.
(these are my affiliate links)
***********Math, Physics, and Computer Science Books***********
These are my affiliate links. As an Amazon Associate I earn from qualifying purchases.
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
(these are my affiliate links)
***********Math, Physics, and Computer Science Books***********
These are my affiliate links. As an Amazon Associate I earn from qualifying purchases.
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
Group Homomorphisms Map the Identity to the Identity (Proof)
Proof: Basic Properties of Homomorphisms (Identities and Inverses) | Abstract Algebra
Group Homomorphisms Map Inverses to Inverses | Abstract Algebra Exercises
The Kernel of a Group Homomorphism – Abstract Algebra
Group Homomorphisms Preserve Identities | Abstract Algebra Exercises
Intro to Group Homomorphisms | Abstract Algebra
Group Homomorphism and Isomorphism
Prove that Every Group Homorphism Maps the Identity Element to the Identity Element
Group Homomorphisms - Abstract Algebra
【Abstract Algebra I Lecture 7】Group Homomorphisms I - MAT211 | Nge Kie Seng 20231009
GT8. Group Homomorphisms
【Abstract Algebra I Lecture 8】Group Homomorphisms II - MAT211 | Nge Kie Seng 20231011
Abstract Algebra 56: Example group homomorphisms
Chapter 6: Homomorphism and (first) isomorphism theorem | Essence of Group Theory
Group Theory Lecture 3.2 Group Homomorphisms
Abstract Algebra - 10.1 Group Homomorphisms and Properties
Abstract Algebra Homomorphisms Kernel is a Subgroup
Properties of Group Homomorphisms
Proving a Function is a Group Homomorphism (Example with the Modulos)
Group Homomorphisms -- Abstract Linear Algebra 4
Kernels of Homomorphisms | Abstract Algebra
29 Group homomorphisms send inverses to inverses
How to Count Group Homomorphisms Between Cyclic Groups
Normal Subgroups and Quotient Groups (aka Factor Groups) - Abstract Algebra
Комментарии
 0:06:53
0:06:53
 0:05:57
0:05:57
 0:03:10
0:03:10
 0:04:53
0:04:53
 0:02:56
0:02:56
 0:15:01
0:15:01
 0:06:03
0:06:03
 0:03:07
0:03:07
 0:10:04
0:10:04
 2:02:45
2:02:45
 0:17:41
0:17:41
 2:01:13
2:01:13
 0:08:31
0:08:31
 0:12:47
0:12:47
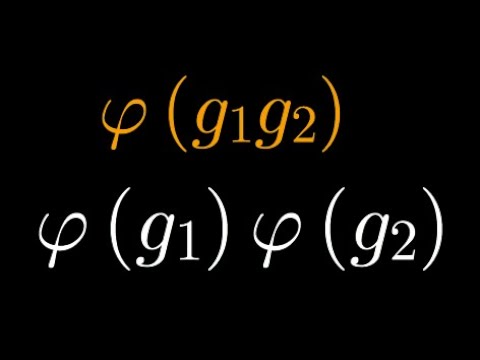 0:27:05
0:27:05
 0:18:03
0:18:03
 0:01:29
0:01:29
 0:13:06
0:13:06
 0:04:21
0:04:21
 0:35:24
0:35:24
 0:11:04
0:11:04
 0:04:23
0:04:23
 0:09:52
0:09:52
 0:11:24
0:11:24