filmov
tv
Every Group of Order Five or Smaller is Abelian Proof

Показать описание
Every Group of Order Five or Smaller is Abelian Proof. In this video we prove that if G is a group whose order is five or smaller, then G must be abelian.
Every Group of Order Five or Smaller is Abelian Proof
5. Order of a group || Finite group || Infinite group || Order of finite group #group #orderofagroup
Group Theory | Special Properties Of Groups of Order 1 to 5
Advanced Algebra (lecture 5.D)| show that a group of order of prime power is nilpotent
Group under addition modulo 5
#04 trick of abstarct algebra | If in a group G , a^5=e ,aba^-1 =b^2 , then order of b is
Abstract Alg Class 5: D3 Cayley Table, Cycle Multiplication (Permutations), Order (Group & Eleme...
Prove set G= {0, 1, 2, 3, 4, 5} is abelian group of order 6, addition modulo 6. | Jayesh Umr
The ABSURD Rules and Engineering Behind Group 5 Special Production | Group 5 Monsters Explained!
The symmetric group -- Abstract Algebra 5
Commutativity and conjugates | Group theory episode 5
Top 5 types of people in the friend group 👀💯
Prove set G= {1, 2, 3, 4, 5, 6} is abelian group of order 6, multiplication modulo 7 | Jayesh
Group theory 5: products
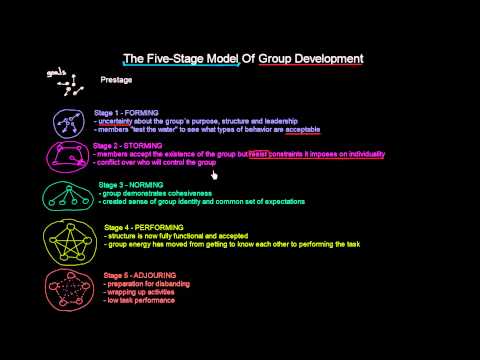
The Five-Stage Model Of Group Development | Organisational Behavior | MeanThat
Shin Megami Tensei 5 Vengeance - ALL Group Skills
Every friend group of five has 🫂💗. #trending #aesthethic #friends
Lecture #27:The Set S={1,3,5,7}is a Group w.r.t Multiplication Modulo 8
Jolly Song Group 5 'z' 'w' 'ng' 'v' 'oo' with acti...
How Far Can Every Tier 5 Group Get? | BTD6
My top 5 songs of every group i stan
All tier 5 group vs fortified BAD in BTD6
Tuckman's 5 Stages of Group Development: Group development in occupational therapy:
Albion Online ALL Floor 5 GROUP BOSSES IN ONE VIDEO + EXTRAS
Комментарии
 0:04:59
0:04:59
 0:02:47
0:02:47
 0:13:02
0:13:02
 0:06:03
0:06:03
 0:08:31
0:08:31
 0:10:05
0:10:05
 0:55:59
0:55:59
 0:11:27
0:11:27
 0:11:30
0:11:30
 0:50:29
0:50:29
 0:26:00
0:26:00
 0:00:38
0:00:38
 0:13:22
0:13:22
 0:29:50
0:29:50
 0:03:55
0:03:55
 0:05:05
0:05:05
 0:00:19
0:00:19
 0:09:12
0:09:12
 0:01:32
0:01:32
 0:15:13
0:15:13
 0:17:42
0:17:42
 0:10:52
0:10:52
 0:13:32
0:13:32
 0:18:30
0:18:30