Proving a Function is a Group Homomorphism (Example with the Modulos)

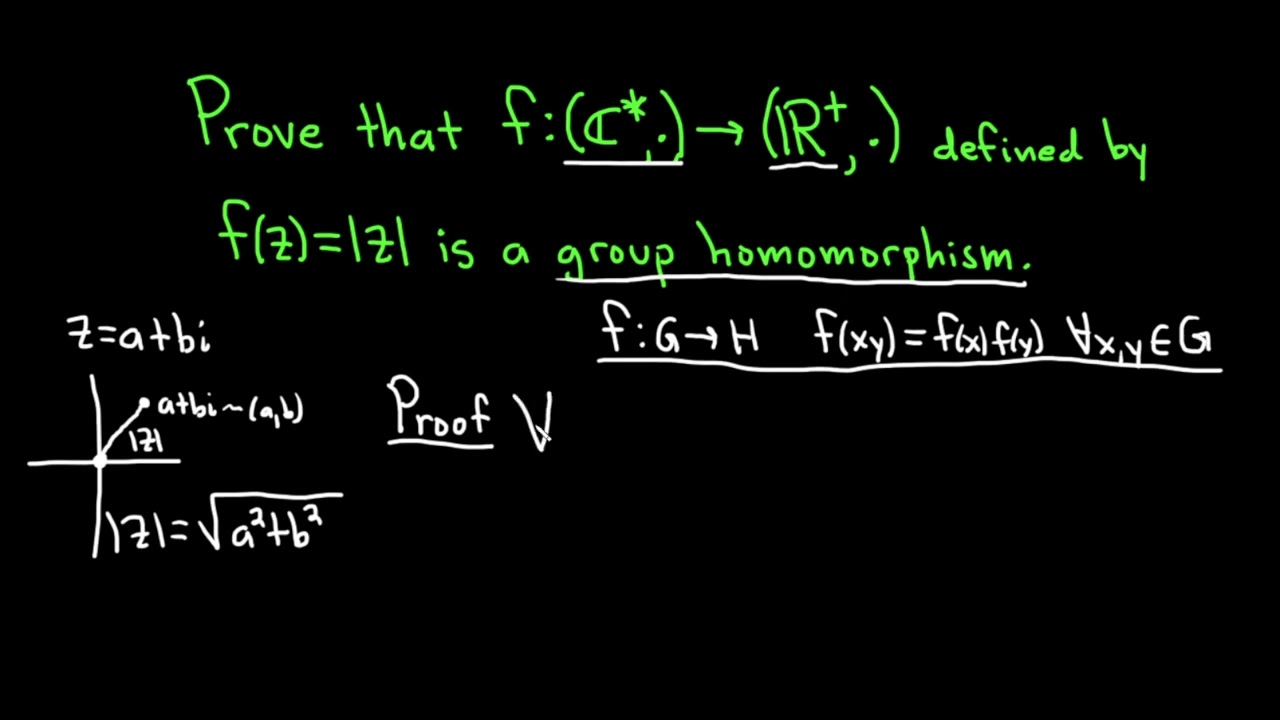
Показать описание

Consider the map that takes the group of nonzero complex numbers under multiplication into the positive reals under multiplication given by f(z) = |z| where |z| is the modulos of z. We prove that this function is a group homomorphism.

(these are my affiliate links)

***********Math, Physics, and Computer Science Books***********
These are my affiliate links. As an Amazon Associate I earn from qualifying purchases.

If you enjoyed this video please consider liking, sharing, and subscribing.

There are several ways that you can help support my channel:)

************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course

Advanced Calculus Course

Calculus 1 Course

Calculus 2 Course

Calculus 3 Course

Calculus 1 Lectures with Assignments and a Final Exam

Calculus Integration Insanity

Differential Equations Course

Differential Equations Lectures Course (Includes Assignments + Final Exam)

College Algebra Course

How to Write Proofs with Sets Course

How to Write Proofs with Functions Course

Trigonometry 1 Course

Trigonometry 2 Course

Statistics with StatCrunch Course

Math Graduate Programs, Applying, Advice, Motivation

Daily Devotionals for Motivation with The Math Sorcerer

Thank you:)

Рекомендации по теме

Комментарии

Thank you for this. More math Proof style videos, please!

masterdistiller

The whole point of this example is proving that the modulo is multiplicative. Skipping that just takes away the interesting part as we're just restating the fact that it is a group homomorphism.

manuelpico

So, you're using C* instead of C/{0}?

coffeeconfessor

Nice video! What sub-branch of math is this from?(I.e where could I learn more?)

johnchristian

Can you make a video on group actions?

blakebates

I don’t even know what group homomorphism is, let alone prove them. 😭

kirstbarcy

Proving a Function is a Group Homomorphism (Example with the Modulos)

How to Prove a Function is Injective(one-to-one) Using the Definition

How to Prove a Function is Surjective(Onto) Using the Definition

Proving a Function is Onto- Discrete Math

How to Prove a Function is Not Surjective(Onto)

Proving a Function is One-to-One and Onto

Proving a function is a probability density function

How to Prove a Function is Surjective | Logic and Proofs

Proving a function is one-to-one-Discrete Math

If a = 5ˣ , b = 5ʸ and aʸ . bˣ = 25 , prove that xy = 1

Proving a Function is One-One

Proving a Function is a Linear Transformation F(x,y) = (2x + y, x - y)

How to Prove a Function is Not an Open Function

Proving A Function Is One To One

How to Prove a Function is a Bijection and Find the Inverse

How to prove a function is onto? | Relations and Functions | Class XII | Mathematics | Khan Academy

How to Prove a Function is a Linear Transformation

Prove the function f:Z x Z → Z given by f(m,n) = 2m - n is Onto(Surjective)

How to Prove the Rational Function f(x) = 1/(x - 2) is Surjective(Onto) using the Definition

Proving a Function is a Group Homomorphism (Example with the Modulos)

Algebra: How to prove functions are injective, surjective and bijective

How to prove a function is increasing?

Proving that a function is increasing

Prove f(x) = x^3 is a bijection. Set Theory. Abstract Algebra

Prove or Disprove if the Function is Injective