filmov
tv
Pi Times Phi using a Regular Icosagon Area (visual proof)
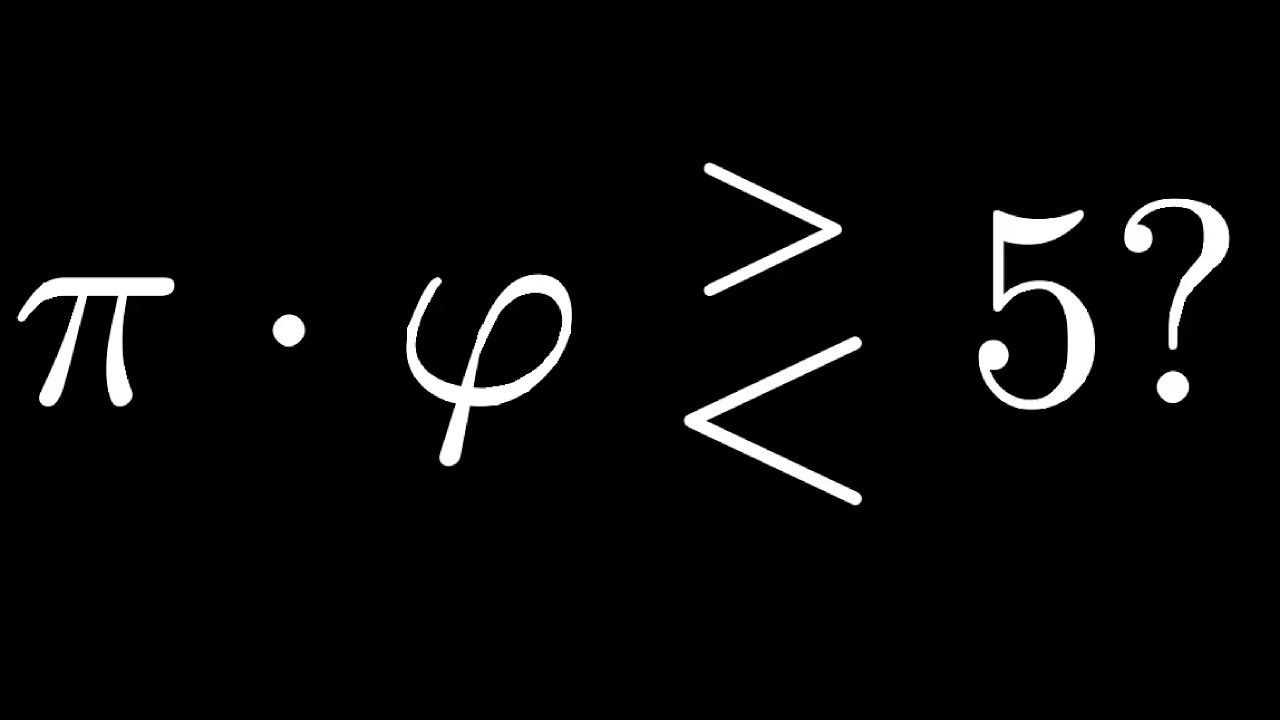
Показать описание
In this video, we use a golden triangle to find the area of a regular icosagon sitting inside of the unit circle (the circle with radius 1). From this area formula, we are able to then find an interesting bound on the product of two famous constants: Pi and the golden ratio.
#math #manim #visualproof #mathvideo #geometry #mathshorts #geometry #mtbos #animation #theorem #pww #proofwithoutwords #proof #iteachmath #icosagon #area #dissection #trigonometry #polygon #sine #pi #goldenratio #phi #goldentriangle #inequality #area
To learn more about animating with manim, check out:
#math #manim #visualproof #mathvideo #geometry #mathshorts #geometry #mtbos #animation #theorem #pww #proofwithoutwords #proof #iteachmath #icosagon #area #dissection #trigonometry #polygon #sine #pi #goldenratio #phi #goldentriangle #inequality #area
To learn more about animating with manim, check out:
Комментарии