filmov
tv
Phi and the TRIBONACCI monster

Показать описание
NEW (Christmas 2019). Two ways to support Mathologer
(see the Patreon page for details)
Today's video is about explaining a lot of the miracles associated with the golden ratio phi, the Fibonacci sequence and the closely related tribonacci constant and sequence.
Featuring the truely monstrous monster formula for the nth tribonacci number, the best golden ratio t-shirt in the universe, rabbits, mutant rabbits, Kepler's wonderful Fibonacci-Phi link, Binet's formula, the Lucas numbers, golden rectangles, icosahedra, snub cubes, Marty, a very happy Mathologer, etc.
Special thanks to my friend Marty Ross for some good-humoured heckling while we were recording the video and Danil Dimitriev for his ongoing Russian support of this channel.
Also check out my other videos featuring the golden ratio and the Fibonacci numbers.
Enjoy!
(see the Patreon page for details)
Today's video is about explaining a lot of the miracles associated with the golden ratio phi, the Fibonacci sequence and the closely related tribonacci constant and sequence.
Featuring the truely monstrous monster formula for the nth tribonacci number, the best golden ratio t-shirt in the universe, rabbits, mutant rabbits, Kepler's wonderful Fibonacci-Phi link, Binet's formula, the Lucas numbers, golden rectangles, icosahedra, snub cubes, Marty, a very happy Mathologer, etc.
Special thanks to my friend Marty Ross for some good-humoured heckling while we were recording the video and Danil Dimitriev for his ongoing Russian support of this channel.
Also check out my other videos featuring the golden ratio and the Fibonacci numbers.
Enjoy!
Phi and the TRIBONACCI monster
Phi and The Fibonacci Sequence Explained
Way beyond the golden ratio: The power of AB=A+B (Mathologer masterclass)
Tribonacci Numbers (and the Rauzy Fractal) - Numberphile
The fabulous Fibonacci flower formula
What is Phi, 1.618, and The Golden Ratio? | Phi in 5 Minutes!
Codewars Javascript, решение задачи Tribonacci sequence
phi universe
What is Phi?
nth term of Tribonacci Series #shorts
9 In Phi & Fibonacci
Tribonacci Numbers | Prof. Glenda R. Tandingan
PHI Number in Nature and Crypto
Mathematics wasn't invented.... it's take from nature
Tribonacci Sequence
Finding Phi
Fibonacci and Tribonacci constant memory solution
Complex Fibonacci Numbers?
Tales of Phi : Math land Great Battle - Battle Difficulties - Ads Video
Master SAT Math 💪| Find the value of phi+1/phi | Golden Ratio
Course in Fibonacci Numbers, Phi, Primes and Astrology
Phi number and Islam ?
Tribonacci Traces 3D
Solving Leetcode 1137. N-th Tribonacci Number
Комментарии
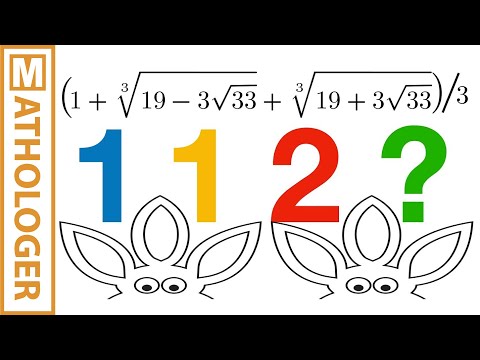 0:20:56
0:20:56
 0:03:38
0:03:38
 0:49:49
0:49:49
 0:07:24
0:07:24
 0:11:27
0:11:27
 0:05:00
0:05:00
 0:08:17
0:08:17
 0:00:15
0:00:15
 0:00:37
0:00:37
 0:00:46
0:00:46
 0:02:36
0:02:36
 0:02:15
0:02:15
 0:00:40
0:00:40
 0:01:00
0:01:00
 0:03:56
0:03:56
 0:05:03
0:05:03
 0:03:16
0:03:16
 0:20:08
0:20:08
 0:00:38
0:00:38
 0:05:41
0:05:41
 0:06:28
0:06:28
 0:09:12
0:09:12
 0:00:31
0:00:31
 0:01:35
0:01:35