Introduction to the Lorentz transformation | Special relativity | Physics | Khan Academy

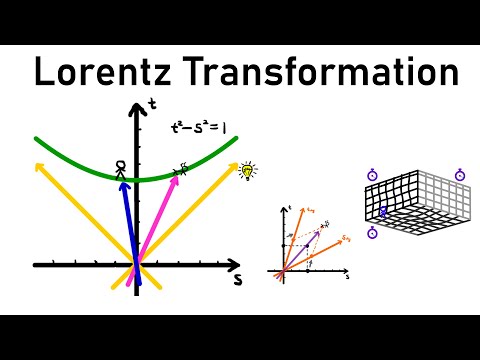
So we've got two coordinate systems from the perspectives of two observers. How can we convert spacetime coordinates between these? Enter the Lorentz transformation!

Physics on Khan Academy: Physics is the study of the basic principles that govern the physical world around us. We'll start by looking at motion itself. Then, we'll learn about forces, momentum, energy, and other concepts in lots of different physical situations. To get the most out of physics, you'll need a solid understanding of algebra and a basic understanding of trigonometry.

About Khan Academy: Khan Academy offers practice exercises, instructional videos, and a personalized learning dashboard that empower learners to study at their own pace in and outside of the classroom. We tackle math, science, computer programming, history, art history, economics, and more. Our math missions guide learners from kindergarten to calculus using state-of-the-art, adaptive technology that identifies strengths and learning gaps. We've also partnered with institutions like NASA, The Museum of Modern Art, The California Academy of Sciences, and MIT to offer specialized content.

For free. For everyone. Forever. #YouCanLearnAnything

[christianlorentz]

there's no way in hell any of my bloodline came up with this :0

[TTTRJinsei]

I laughed so hard on how the way he stress out the word *SPACETIME*

[waqqiali]

For those who are still wondering about the alpha formula:

Drop a perpendicular from ct' axis to ct axis because ct' axis is the relative motion of your friend. And then from this right angle triangle you will get the perpendicular "x" and the base "ct". Then you can do the following:

tan(α)=P/H
tan(α)=x/ct=(x/t)(1/c)
tan(α)=v/c
α=arctan(v/c).

[outerprobe]

i like how the guy pronounce 'space-tiME!' !1!

[learningschool]

I don’t see how alpha is equal to inverse tangent of v/c

[thunorwodenson]

They couldve called it timace but then it would sound like an enzyme.

[nilau]

The more I understand it the more it feels weird to move.. the imagination that I'm changing spacetime just a tiny tiny tiny tiny tiny tiny bit is odd/awesome at the same time! Thank you Sir, GREAT tutorial!

[Kappa]

spacetimee, sounds so joyful when you say it

[ericabutts]

how many times he says ..SPACETIME....

[sxu]

I came across lorentz tranformation in reading six uneasy pieces by Richard Fayman. Nice explanation from a different source.

[evenaicantfigurethisout]

2:16 why does he say "this angle, we've already seen .." but we've not actually seen it yet. i've watched all the videos before this. the last video before this being "angle of x' axis in minkowski spacetime". none of the prior videos have we derived this angle alpha.

[JuneJulia]

So impressed how he can write so well with mouse.
Even better than my pen hand-writing.

[elissabell]

Does anyone know why the angle α = tan^-1(v/c) ?

[pinghaodong]

Is he the guy dubbed Jerry Smith in Rick and Morty

[muhammadumar]

Thank you so much sir,
You have beaten Brian Green in teaching according to me. I was very much confused by all these stuff but today it's clear. Thank you Sir
Love from PAKISTAN

[whysorandom]

This was such a good explanation, thank you

[terlinguabay]

I listened to this with my eyes closed, and loved it
Well done.

[DanielSantos-nzpp]

where did a=arctan(v/c) come from? Looking for it Khan's other videos about spacetime. Must've missed it

[JASONQUANTUM]

Lorentz invariance is a fundamental principle in physics, stating that the laws of physics are the same for all observers moving at a constant velocity relative to each other. In the context of QIH, the equation H∣ψ⟩ = iℏ∂∂t∣ψ⟩ = GμνTμν = k * ln(W) plays a significant role.

This equation, which relates the Hamiltonian operator (H) to the time evolution of a quantum state (∣ψ⟩), the Einstein tensor (Gμν) to the energy-momentum content (Tμν), and the quantum information content (W), implies a deep connection between quantum mechanics and gravity. It suggests that the underlying information encoded within quantum states and spacetime curvature is consistent across reference frames, regardless of their relative motion.

Lorentz invariance ensures that the equation's fundamental principles remain unchanged as long as transformations are applied consistently to the terms involving quantum information (k * ln(W)) and to the terms involving spacetime curvature (GμνTμν). This consistency between quantum information and spacetime curvature across different reference frames preserves the equation's integrity under Lorentz transformations.

This mutual consistency is one of the key strengths of QIH. It indicates that the interplay between quantum mechanics and gravity, as encapsulated in the equation, remains invariant regardless of the observer's motion. By capturing the intricate connections between quantum states, information, and spacetime curvature, QIH offers a framework where the underlying information serves as a bridge that unifies quantum mechanics and gravity in a Lorentz-invariant manner. (Send me the Nobel when you get a chance ;)

[ANJA-mjto]

Than you because I can better understand the amplitude of a damped harmonic osillator and corresponding spectrum line profil for a Lorentz - function with FWHM. This would be guid for the shape of a spectrum line emitted by an attomic transmition if the atoms were held perfectly still while they emitted.