Derive Lorentz Transformations

Can you Derive the Lorentz Transformations from the postulates of STR?

When two inertial observers look at a common event, their measurements of distances and time are related by transformation equations. Usually, we use Galilean transformation (GT) equations.

However, the GT are not compatible with the postulates of Special Theory of Relativity. It cannot predict that the speed of light is a constant. It also cannot accommodate relativistic phenomenon like length contraction, time dilation, etc.

For this reason, GT needs to be replaced with a new set of transformation equations that will be compatible with Special Relativity.

These are called Lorentz Transformations.

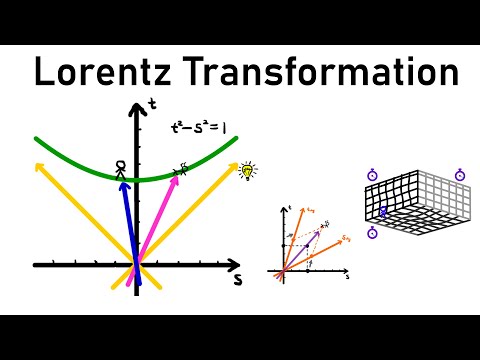
In this video, I derive the Lorentz transformations for a very simple case, where relative motion between both frames of reference is happening only in one direction.

STAY TUNED. PEACE...

𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬
Your financial support provides me an additional incentive to create high quality lecture videos. I am very much thankful for your generosity and kindness

JOIN as a member in Youtube 😇😇😇
𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬𓏬

PLAYLIST ON Special Theory of Relativity
-----------------------------------------------------
-----------------------------------------------------

[FortheLoveofPhysics]

PLAYLIST ON Special Theory of Relativity - Lecture Series

[thewormholetv]

I feel really bad when I see rubbish videos on YouTube getting veiws and really good videos like you made get much less views, it frustrates me so much!! Believe me I like you're every video really talented youtuber you deserve a million likes.

[salauddeensyed]

I am 65 years old and am a retired engineer. But let me address you as Guruji.
Thank you Guruji, for explaining Lorentz transformation in simple and clear terms. May God bless you...

[lukecasey]

"Are you understanding?" lmao.
No but thank you very much for this really helpful video.
I am understanding ;)

[ozzyfromspace]

I literally signed in just to leave this comment: you're a phenomenal lecturer, you improved my understanding of the Lorentz transformation. Especially the part about how an inertial frame shouldn't impart an acceleration when you go from one frame to another. It makes total sense, but I never realized it, so I couldn't understand why special Relativity assumes the homogeneity of space and time (what you gracefully call Linearity). Thanks mate, this video is exactly what I needed! Greetings from the US ☺️🙏🏽🎉

[FortheLoveofPhysics]

What is Time Dilation?
What is Length Contraction?
What is Relativity of Simultaneity?

[Thenonselectedaspirant]

sir can you please make some videos for IIT JAM

[khansubiya]

I searched Lorentz eqn and YouTube came up with so many videos.I saw few but wasn't satisfied then I saw urs and i can't say how much happy I was becoz I was able to understand every bit of it.U have such a proficient English which helped a lot to understand with clarity.Nothing can be more fulfilling than getting a conceptual clarity.Thanku sir.

[anjali]

Amazing explanation⚡⚡.... You explain everything very clearly,
Thankyou sirfor this wonderful video 💫💫

[mohammedheneen]

Amazing.. very useful lessons
I really like your videos .. Please keep going ..
All respect
👍👍👍

[shadyirish]

Sir, you are a Legend. My professor just told me some abstract way of doing this which no one in class understood. However this 26 minute video did what he couldn't do in 2 hours of lecture.

[toobanazirf]

You explain everything in such a beautiful way that there's no contradiction or misconception left about the video at the end of lecture.. thank you Soo much from Pakistan 🇵🇰

[manaoharsam]

I am a retired Engineer as well. 9 yrs ago I read derivation of Lorentz transformation. Today I revisited again. I have to say I enjoyed your video.

Excellent video.

[girishtripathy]

Hell a lot of videos on Youtube regarding this derivation. I finally now understood the Thing. Thanks Sir.! <3 you the best

[yuval]

C the speed of light is constant; 't only increases (from the moment of the merger of 'S and S) while 'x decreases in value;
How then does c multiplied by 't decrease in value,

[tursinbayoteev]

To derive reverse transform at 10:53 is assumed that the event happened at x=0 at the origin of the S frame. For S' frame, it is x'=-v*t. When x'=a*x+v*t is used for this, I got x=(x'+v*t')/a not x=(x'+v*t')a. What is wrong?

[speedster]

I'm a lecturer, this is an amazing presentation, the fact that you simplify such a complicated subject is a brilliant

[lifestylelifestyle]

thank you so much for this explication i understand well now thank from Morocco

[The_Green_Man_OAP]

You should check out the John Chappell science talks. (John Chappell Natural Philosophy Society).
– They'd love to host someone like you, to explain Relativity to them in a clear way.

[rbwinn]

I think it is wonderful that you love physics. What I would like to see is a person in science who loves the axioms of algebra. You are wrong when you say the Galilean transformation equations cannot show constant speed of light. Consider a clock in a flying airplane. Einstein says that clock will be slower than an identical clock on the ground. Here are the Galilean transformation equations.
x'=x-vt
y'=y
z'=z
t'=t
If t is the time of the clock on the ground, then obviously, t' cannot be the time of the slower clock in the airplane. You would have to use another set of Galilean transformation equations with different variables for velocity and time. So the inverse equations would be
x = x' - (-vt/n')n'
y = y'
z = z'
n = n'
n' is the time of the slower clock in the airplane. (-vt/n') is the velocity of the ground relative to the airplane according to the time of the clock that shows n'
. n = n' shows that the time of the slower clock in the airplane is being used in both frames of reference. So to show constant speed of light, we just say x=ct and x'=cn'.
It does not matter whether n' is a slower or faster clock than the clock that shows t. All that matters is that x'=cn', or in other words, the speed of light is c according to the time of the clock that shows n'. There is no length contraction. If n' is a slower clock, the velocity according to the time of that clock is (-vt/n'), a faster velocity. If n' is a faster clock, the velocity according to the time of that clock is
(-vt/n'), a slower velocity. This all agrees with the first set of Galilean transformation equations because no matter what n' is, the (n')'s cancel out, and we have
x = x' - (-vt)
x = x' + vt
which is the same as our original equation and also the same as
x = x' + vt'
t = t'
What scientists are doing today is the same thing Ptolemy did. Ptolemy had a complicated set of equations that could accurately predict the positions of the planets in the sky, but they showed the planets orbiting the earth in orbits that were epicycles, whereas, the planets were actually orbiting the sun in elliptical orbits. I have yet to see the scientist who will answer this.