filmov
tv
A (correct proof) of 0.99=1 | Sequences and Limits | Math Basics | Math2Go

Показать описание
In this video we will look into the well known fact that 0.99 period ("repeating") equals 1! As alot of proofs out there are mathematically wrong, we will take a different approach and prove the statement using sequences and limits.
Playlists:
If you have any questions please feel free to ask. You can also ask for specific other mathematical problems in the comment section below!
Please comment and subscribe if this video was helpful to you and you wan to stay tuned for more helpful math videos!
Playlists:
If you have any questions please feel free to ask. You can also ask for specific other mathematical problems in the comment section below!
Please comment and subscribe if this video was helpful to you and you wan to stay tuned for more helpful math videos!
A (correct proof) of 0.99=1 | Sequences and Limits | Math Basics | Math2Go
Does 0.999... = 1?
0.9 Repeating Equal to 1 Algebraic Proof | Fun Math JusticeTheTutor #shorts #maths #math
Every PROOF you've seen that .999... = 1 is WRONG
Pizza proof 0.999... = 1
Simple Proof That 0.99 Repeating Is Equal To 1:
Proving 0.9999....=1 A marvellous proof #shorts
Infinite Math Test (Proof that 0.999... = 1)
Simplest proof that 0 999 is not equal to 1
1/0 = Undefined or Infinity: Easy proof to understand with a real world example
1 + 1 = 3 Proof | Breaking the rules of mathematics
MATH: Explaining Formal Proof that .999... = 1
proof you’re not ugly😳 #confidence #shorts
0.9 Repeating Equal to 1 Algebraic Proof | Fun Math #shorts #maths #mathstricks #priyanka_prajapati
Pee Safe XXL Ultra Thin Sanitary Pads | Leak proof Sanitary Napkins | Extra Long Ultra Thin Pads
I Learned How to Divide by Zero (Don't Tell Your Teacher)
'99 Percent' Miss This. What Is The Length?
The Simple Question that Stumped Everyone Except Marilyn vos Savant
Fortnite makes no sense...
Spanish Mathematical Olympiad | Can You Proof 1/a^1999+1/b^1999 +1/c^1999=1/(a^1999 +b^1999+c^1999)
NASA ROVER SPOTS ALIENS | The Proof Is Out There | #Shorts
The Beautiful Peacock 1 Oz Gold Proof Coin #peacock #gold #emkcoins
Proof Air Purifier WORKS 🌬 #watchthis 👀
258. Add Digits | O(1) with Mathematical Proof | LeetCode Daily Challenge | LeetCode POTD
Комментарии
 0:04:37
0:04:37
 0:02:27
0:02:27
 0:01:01
0:01:01
 0:09:25
0:09:25
 0:00:57
0:00:57
 0:01:00
0:01:00
 0:00:29
0:00:29
 0:06:02
0:06:02
 0:01:59
0:01:59
 0:04:14
0:04:14
 0:08:25
0:08:25
 1:02:41
1:02:41
 0:00:12
0:00:12
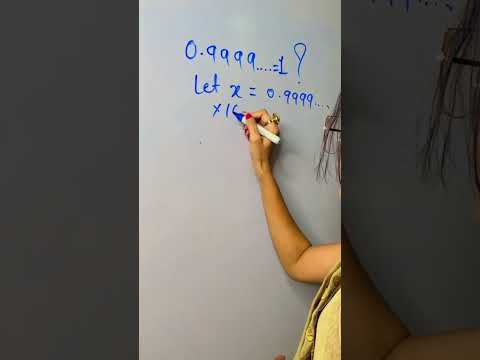 0:00:18
0:00:18
 0:00:25
0:00:25
 0:07:36
0:07:36
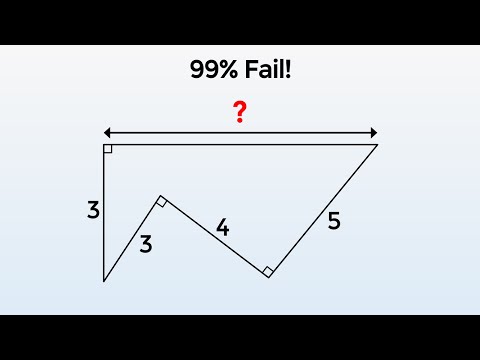 0:03:49
0:03:49
 0:07:06
0:07:06
 0:00:15
0:00:15
 0:07:54
0:07:54
 0:00:41
0:00:41
 0:00:08
0:00:08
 0:00:09
0:00:09
 0:09:32
0:09:32