filmov
tv
Deriving the Wave Equation

Показать описание
In this video I derive the Wave Equation, one of the most important and powerful partial differential equations. It can be used for a huge variety of other problems in physics and engineering. In the next few lectures, we will solve and analyze this equation. Examples from a guitar string are used to illustrate ideas.
@eigensteve on Twitter
This video was produced at the University of Washington
%%% CHAPTERS %%%
0:00 Overview
2:00 The Wave Equation and Examples
8:33 History of the Wave Equation
10:03 Deriving the Wave Equation from F=ma
25:25 Quick Recap of Derivation
31:53 The Wave Equation and the Guitar String
35:08 Conclusions and Next Videos
@eigensteve on Twitter
This video was produced at the University of Washington
%%% CHAPTERS %%%
0:00 Overview
2:00 The Wave Equation and Examples
8:33 History of the Wave Equation
10:03 Deriving the Wave Equation from F=ma
25:25 Quick Recap of Derivation
31:53 The Wave Equation and the Guitar String
35:08 Conclusions and Next Videos
Deriving the Wave Equation
Wave Equation Derivation - Transverse Waves on a String
The Wave Equation for BEGINNERS | Physics Equations Made Easy
Deriving the Universal Wave Equation
Introducing the Wave Equation: Derivation and Intuition
The equation of a wave | Physics | Khan Academy
Two Ways to Derive the Wave Equation
Derivation of the 1D Wave Equation
Wave Equation
The Schrödinger Equation Explained in 60 Seconds
Wave equation with damping & forcing: derivation for a string
Sinusoidal wave equation
Drinking and Deriving | Maxwells Wave Equations
Electromagnetic Wave Equation in Free Space
Wave Equation | Waves | Physics | FuseSchool
Wave Equation
Ch 13: Where does the Schrödinger equation come from? | Maths of Quantum Mechanics
Quantum Wavefunction | Quantum physics | Physics | Khan Academy
Why does v=fλ? Derivation of the wave equation.
How This Equation Describes All Waves Around Us (+ the Most Boring Solution) - Parth G Wave Equation
Schrodinger Equation. Get the Deepest Understanding.
Derivation of one dimensional wave equation | VTU Mathematics | Module 3
How to derive the wave equation (PDE)
How Schrodinger Came Up With His Famous Equation (But EASIER)
Комментарии
 0:35:56
0:35:56
 0:16:44
0:16:44
 0:16:59
0:16:59
 0:01:37
0:01:37
 0:10:34
0:10:34
 0:14:43
0:14:43
 0:28:49
0:28:49
 0:26:17
0:26:17
 0:15:14
0:15:14
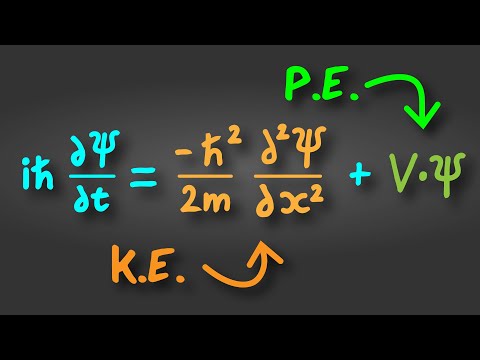 0:01:00
0:01:00
 0:12:58
0:12:58
 0:07:27
0:07:27
 0:09:56
0:09:56
 0:08:34
0:08:34
 0:03:24
0:03:24
 0:04:48
0:04:48
 0:14:58
0:14:58
 0:10:11
0:10:11
 0:02:06
0:02:06
 0:08:59
0:08:59
 0:49:30
0:49:30
 0:12:12
0:12:12
 0:08:30
0:08:30
 0:10:35
0:10:35