filmov
tv
How This Equation Describes All Waves Around Us (+ the Most Boring Solution) - Parth G Wave Equation

Показать описание
What does it mean to "solve" the Wave Equation? And why is the most boring solution so important?
In this video, we will take a look at what is known as the wave equation. In reality, there are a few different equations in physics (even in classical physics) that describe wave behavior, but the one we will look at describes the most basic classical waves, and is thus known as THE wave equation. It describes classical waves such as sound waves, electromagnetic waves, and water waves. The wave equation is a second-order partial differential equation, and in this video we will take a look at the 1 dimensional version.
The equation itself says that the second order partial derivative with respect to time, of the displacement of the wave medium, is equal to the square of the wave speed multiplied by the second order partial derivative of the displacement with respect to our spatial direction. In the video we see how this is represented by all the symbols. We also understand differentiation (and derivatives) as taking the gradient of our u function (displacement) at every point. The partial derivatives ensure we keep other variables constant.
Solving the wave equation just means finding a function for u (displacement of the wave medium) that satisfies the equation. Beyond this, there are many possible solutions. The most basic one we usually study is a sinusoidal solution, both in time and in space. We will look at the mathematical form of this kind of solution. It's also interesting to note that many different kinds of sinusoid (i.e. with different amplitudes, frequencies, and phases) are allowed as solutions to the equation. These solutions are generally found using some tedious algebraic methods, such as separation of variables - very interesting mathematically, but not quite our focus as physicists.
The wave equation is what is known as a linear equation. Therefore, by the Principle of Superposition, any two solutions can be added together to find another solution. If we reverse this logic, we can say that complicated waves that are not necessarily sinusoidal in nature can be broken down into a sum of component sine waves, meaning they must be allowed solutions to the wave equation due to its linearity.
An excellent example of this is when two identical waves travel in opposite directions towards each other. The resultant wave (what is seen when these waves overlap) is known as a standing wave. It appears to not travel in either direction, but rather just oscillate between zero amplitude and maximum amplitude at the same region in space. The standing wave is another solution to the wave equation as it is made of two simpler solutions (the two waves travelling in opposite directions).
And lastly, we see that there is a very boring and trivial solution to the wave equation, which is u = 0. This represents there not being a wave in the region of space and time that we are studying, and easily fits the wave equation, which in this case becomes 0 = 0. However, this solution is very important. Because if it did not solve the wave equation, then this would be indicating that the wave equation does not permit any region of space and time where a wave does not exist. This would be a problem as the wave equation would then not be a good model of our real universe.
Here are some useful resources for understanding how we actually go about solving the wave equation, mathematically speaking:
Thanks so much for watching - please do check out my socials here:
Instagram - @parthvlogs
Music Chanel - Parth G's Shenanigans
Many of you have asked about the stuff I use to make my videos, so I'm posting some affiliate links here! I make a small commission if you make a purchase through these links.
Timestamps:
0:00 - Understanding The Wave Equation in 1 Dimension
2:10 - Second Order Partial Derivatives Explained
3:43 - What Does it Mean to "Solve" the Wave Equation?
4:41 - What Do Basic Solutions Look Like?
5:08 - The Linearity of the Wave Equation (and Principle of Superposition)
6:55 - The Most Boring (and Most Important) Solution
In this video, we will take a look at what is known as the wave equation. In reality, there are a few different equations in physics (even in classical physics) that describe wave behavior, but the one we will look at describes the most basic classical waves, and is thus known as THE wave equation. It describes classical waves such as sound waves, electromagnetic waves, and water waves. The wave equation is a second-order partial differential equation, and in this video we will take a look at the 1 dimensional version.
The equation itself says that the second order partial derivative with respect to time, of the displacement of the wave medium, is equal to the square of the wave speed multiplied by the second order partial derivative of the displacement with respect to our spatial direction. In the video we see how this is represented by all the symbols. We also understand differentiation (and derivatives) as taking the gradient of our u function (displacement) at every point. The partial derivatives ensure we keep other variables constant.
Solving the wave equation just means finding a function for u (displacement of the wave medium) that satisfies the equation. Beyond this, there are many possible solutions. The most basic one we usually study is a sinusoidal solution, both in time and in space. We will look at the mathematical form of this kind of solution. It's also interesting to note that many different kinds of sinusoid (i.e. with different amplitudes, frequencies, and phases) are allowed as solutions to the equation. These solutions are generally found using some tedious algebraic methods, such as separation of variables - very interesting mathematically, but not quite our focus as physicists.
The wave equation is what is known as a linear equation. Therefore, by the Principle of Superposition, any two solutions can be added together to find another solution. If we reverse this logic, we can say that complicated waves that are not necessarily sinusoidal in nature can be broken down into a sum of component sine waves, meaning they must be allowed solutions to the wave equation due to its linearity.
An excellent example of this is when two identical waves travel in opposite directions towards each other. The resultant wave (what is seen when these waves overlap) is known as a standing wave. It appears to not travel in either direction, but rather just oscillate between zero amplitude and maximum amplitude at the same region in space. The standing wave is another solution to the wave equation as it is made of two simpler solutions (the two waves travelling in opposite directions).
And lastly, we see that there is a very boring and trivial solution to the wave equation, which is u = 0. This represents there not being a wave in the region of space and time that we are studying, and easily fits the wave equation, which in this case becomes 0 = 0. However, this solution is very important. Because if it did not solve the wave equation, then this would be indicating that the wave equation does not permit any region of space and time where a wave does not exist. This would be a problem as the wave equation would then not be a good model of our real universe.
Here are some useful resources for understanding how we actually go about solving the wave equation, mathematically speaking:
Thanks so much for watching - please do check out my socials here:
Instagram - @parthvlogs
Music Chanel - Parth G's Shenanigans
Many of you have asked about the stuff I use to make my videos, so I'm posting some affiliate links here! I make a small commission if you make a purchase through these links.
Timestamps:
0:00 - Understanding The Wave Equation in 1 Dimension
2:10 - Second Order Partial Derivatives Explained
3:43 - What Does it Mean to "Solve" the Wave Equation?
4:41 - What Do Basic Solutions Look Like?
5:08 - The Linearity of the Wave Equation (and Principle of Superposition)
6:55 - The Most Boring (and Most Important) Solution
Комментарии
 0:08:59
0:08:59
 0:14:54
0:14:54
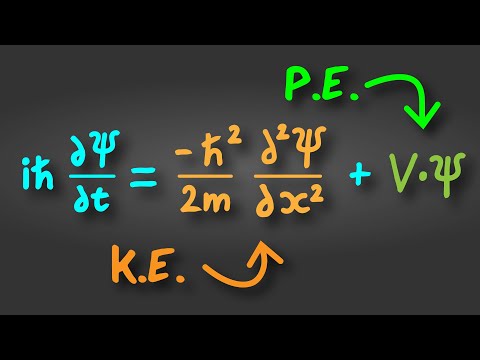 0:01:00
0:01:00
 0:16:43
0:16:43
 0:23:16
0:23:16
 0:13:17
0:13:17
 0:00:56
0:00:56
 0:31:42
0:31:42
 0:21:42
0:21:42
 0:27:16
0:27:16
 0:21:30
0:21:30
 0:23:15
0:23:15
 0:00:20
0:00:20
 0:03:35
0:03:35
 0:02:09
0:02:09
 0:00:45
0:00:45
 0:04:37
0:04:37
 0:01:01
0:01:01
 0:00:30
0:00:30
 0:10:40
0:10:40
 0:36:47
0:36:47
 0:02:14
0:02:14
 0:09:46
0:09:46
 0:09:35
0:09:35