filmov
tv
Wave equation with damping & forcing: derivation for a string
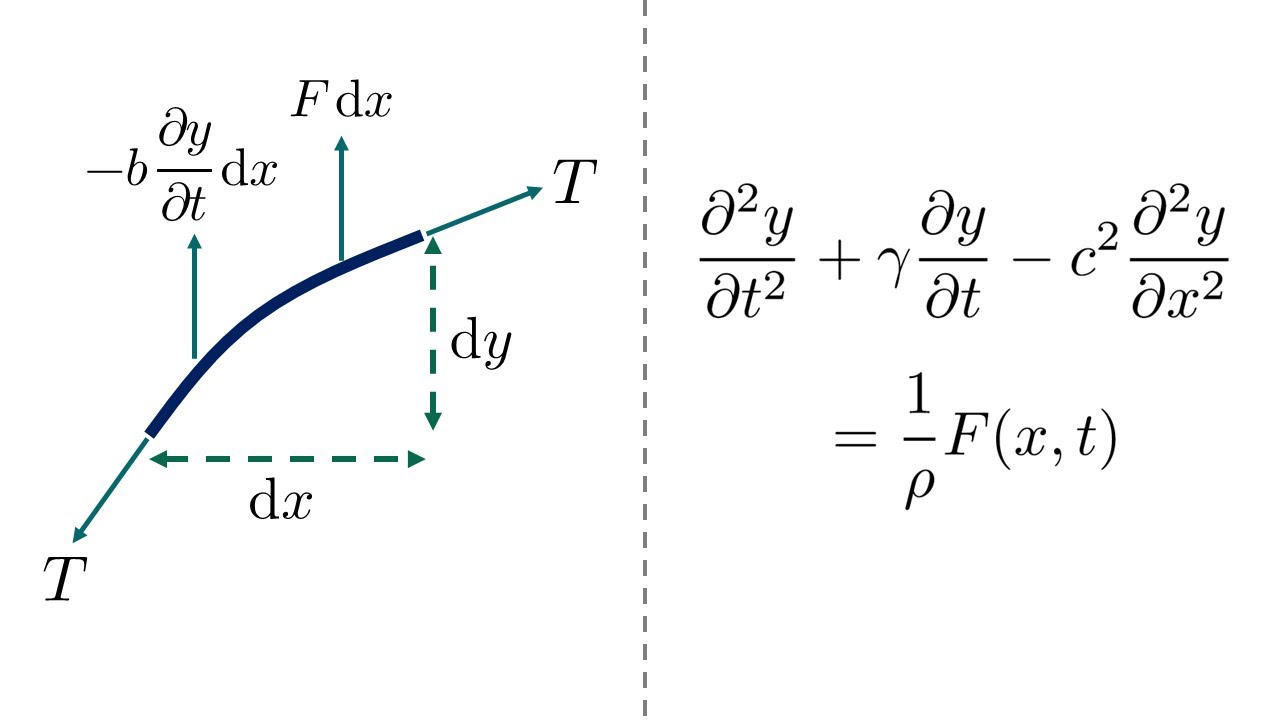
Показать описание
Using Newton's second law to derive the wave equation for a string undergoing small transverse displacements, including the effects of damping and external forces. We'll consider how to solve the resulting partial differential equation in future videos!
About me: I studied Physics at the University of Cambridge, then stayed on to get a PhD in Astronomy. During my PhD, I also spent four years teaching Physics undergraduates at the university. Now, I'm working as a private tutor, teaching Physics & Maths up to A Level standard.
#physics #waves #differentialequation #partialdifferentialequation #partialderivatives #newtonslaws #damping #dissipation #string #tension #calculus #mathematics #maths #math #science #education
About me: I studied Physics at the University of Cambridge, then stayed on to get a PhD in Astronomy. During my PhD, I also spent four years teaching Physics undergraduates at the university. Now, I'm working as a private tutor, teaching Physics & Maths up to A Level standard.
#physics #waves #differentialequation #partialdifferentialequation #partialderivatives #newtonslaws #damping #dissipation #string #tension #calculus #mathematics #maths #math #science #education
Wave equation with damping & forcing: derivation for a string
Solving the damped wave equation on a semi-infinite string
The damped wave equation with unbounded and singular damping by Petr Siegl
Two-dimensional wave equation with damping
Numerical simulation of damped wave equation I
Damped Wave Equation for Physics of Rock
2D wave equation with damping
Oscillations 3 wave equation
Wave equation with damping on a circle
Numerical simulation of damped wave equation II
Deriving the Wave Equation
Transmission lines: deriving the damped wave equation
Simulation - Damped Wave Equation
Damping of Transverse Wave 😎Impressive Physics 🔥 #jee #physics #jeeshorts #namokaul
S10/12. Momentum Neural ODE and Wave equation with viscous damping
Solving the Wave Equation with Separation of Variables... and Guitar String Physics
Wave Equation
The Physics of Damped Harmonic Oscillations: Simplified | Equations of Motion & Beyond
1D Damped Wave Equation
ECE4448 L2: The 1-D Wave Equation for Vibrating Strings (Guitar Amplification & Effects)
One-Dimensional Wave (String) Equation — with Damping Matlab Video - ME 702 Semester Project
Wave equation: general solution via Fourier transform
Damping wave
The Telegraph Equation, Waves and Damped Vibrations of Elastic Strings (Including Guitar Physics)
Комментарии
 0:12:58
0:12:58
 0:16:04
0:16:04
 0:37:45
0:37:45
 0:00:40
0:00:40
 0:00:17
0:00:17
 3:15:41
3:15:41
 0:00:41
0:00:41
 0:07:54
0:07:54
 0:00:30
0:00:30
 0:00:17
0:00:17
 0:35:56
0:35:56
 0:21:02
0:21:02
 0:03:01
0:03:01
 0:00:11
0:00:11
 2:38:47
2:38:47
 0:46:28
0:46:28
 0:15:14
0:15:14
 0:40:24
0:40:24
 0:00:12
0:00:12
 0:19:12
0:19:12
 0:00:26
0:00:26
 0:11:17
0:11:17
 0:29:18
0:29:18
 1:33:29
1:33:29