Euler's Formula: Basic Application & Formula Derivation (Calculus Approach)

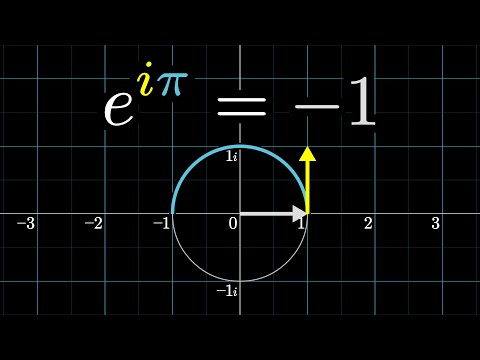
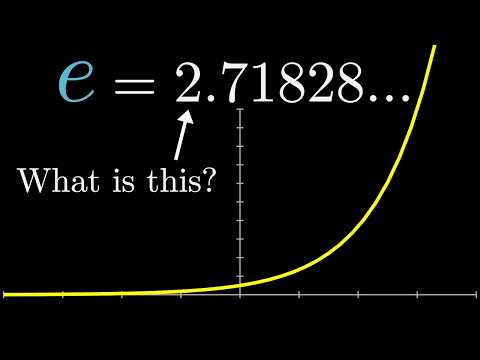
Examine the exciting derivation of the Euler's formula using calculus. Also, see basic applications of this formula (one, leading to the most "beautiful equation of mathematics", having the 5 famous constants: 0, 1, e, pi and i).

This video lays the foundation for other video(s) on Euler's application.

I very recently have to come to learn that the name "Euler" is correctly pronounced "Oy-ler". One learns something new everyday! (7/7/2023).

Must know material for any serious calculus student. Thank you for your attention!

The purpose of the channel is to learn, familiarize, and review the necessary precalculus and trigonometry/geometry topics that form a basis for calculus (with a focus on functions). Calculus topics include limits, derivatives, integrals, formula derivations, derivations/proofs, area/volumes of curves and calculus applications.

Utilize simple and easy techniques to get the material across to you.

Disclaimer: I am not a professor by profession.
Thank you!

#complexnumbers #eulerstheorem #eulersformula #calculusapplications #calculusfundamentals #calculus #derivatives #derivations #functions #professorcalculish #imaginarynumber #eulersidentity #differentialcalculus

[toffeetoe]

Thanks for presenting this formula derivation....it did not seem too complex with the way it was handled.

[박영준-ok]

hi, i am from korea, you know bts from, , , ,

thanks for a lecture
in my high shcool, i didn.t know the euler's forula
but when i am going to unversity, i know a little math
but i have been never thought the prove "constans"
your lecture is simply understanding math
i got it

[lapicethelilsusboy]

This video does not derive the formula. Instead, it confirms the equality. I know 3 different ways to show that e^ix = cos(x)+i.sin(x). By limits, derivative of e^ix on the complex plane and McLaurin's expansion.