filmov
tv
Properties of Matrix Algebra - Proofs

Показать описание
Properties of determinants of matrices | Lecture 31 | Matrix Algebra for Engineers
Linear Algebra 54, Properties of Matrix Algebra
1.4 - Inverses; Algebraic Properties of Matrices (Part 1)
Linear Algebra - Matrix Operations
Matrix Multiplication and Associated Properties
Intro to Matrices
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Inverse Matrices and Their Properties
Linear Algebra 1.4 Inverses; Algebraic Properties of Matrices
Properties of Matrix Algebra - Proofs
Linear Algebra 3.2.1 Properties of Determinants
Properties of the transpose of a matrix, linear algebra tutorial
Linear Algebra 4.3.2 - Standard Properties of Matrix Operations (Video 1 of 2)
Properties of Determinants - Linear Algebra
Dear linear algebra students, This is what matrices (and matrix manipulation) really look like
Properties of Determinants 1
Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebra
The determinant | Chapter 6, Essence of linear algebra
Determinant of 3x3 Matrices, 2x2 Matrix, Precalculus Video Tutorial
[Linear Algebra] Matrix Transposes and Properties
Linear Algebra 17 | Properties of the Matrix Product
Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra
Properties of Matrix Transformations
Types of Matrices with Examples
Комментарии
 0:15:21
0:15:21
 0:03:58
0:03:58
 0:20:16
0:20:16
 0:07:08
0:07:08
 0:06:22
0:06:22
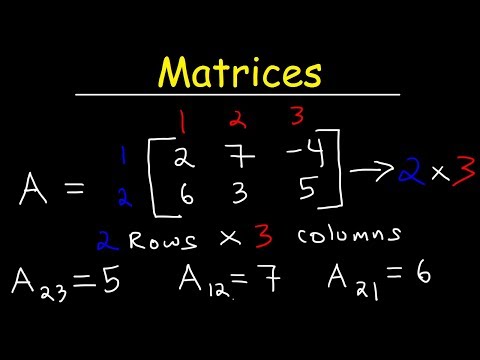 0:11:23
0:11:23
 0:10:59
0:10:59
 0:12:00
0:12:00
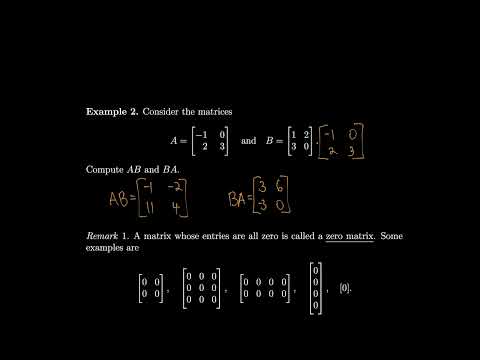 0:42:05
0:42:05
 0:45:12
0:45:12
 0:25:16
0:25:16
 0:13:15
0:13:15
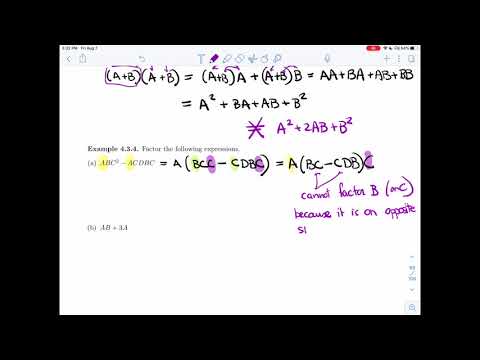 0:11:18
0:11:18
 0:12:15
0:12:15
 0:16:26
0:16:26
 0:02:12
0:02:12
 0:17:16
0:17:16
 0:10:03
0:10:03
 0:10:17
0:10:17
![[Linear Algebra] Matrix](https://i.ytimg.com/vi/jEKLzixQJmI/hqdefault.jpg) 0:07:24
0:07:24
 0:10:50
0:10:50
 0:12:09
0:12:09
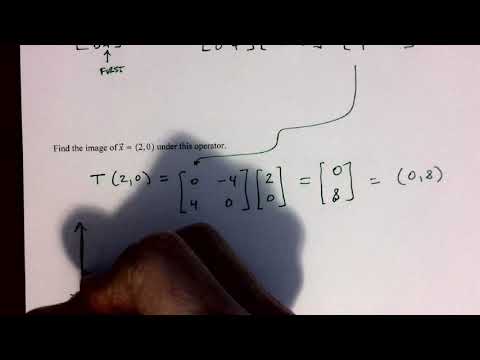 0:36:32
0:36:32
 0:23:37
0:23:37