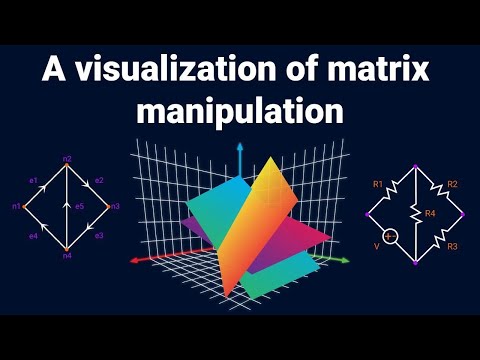
Dear linear algebra students, This is what matrices (and matrix manipulation) really look like

►Follow me

3D Software Used

►My Setup:

[gentlemandude]

I wish someone would explain why linear algebra instructors never motivate the math techniques (re: algorithms) that they teach. Linear algebra is always presented as a set of "recipes" to follow. But students never know whether they're baking a pie, batch of cookies or a cake. This video has provided me with more insight than the semester-long course on Vectors and Matrices that I took in university. It's a shame that linear algebra is taught so poorly. It's such an important topic.

[TheCosmicafroninja]

Adding this visual element is a great idea for helping students to grasp the more intense abstract concepts of mathematics. I felt like I had an okay understanding of linear algebra after taking a class in it but this really helps to solidify my understanding.

[trumanhw]

My god, thank you. It always seemed SO DAMNED ODD when we learned matrices, because in fact, without explaining their contextual utility, it's like teaching about nouns, without telling someone that ... YOU'RE NOT WORKING ON SENTENCES right now -- just nouns. So don't be surprised when nothing sensible occurs from the concept -- because we're not thinking a complete thought ... but rather, accepting that things which look like this can be manipulated in basic basic ways ... in which we'll learn more relevant rules to LATER.

[detonation]

Watching this on the evening before my linear algebra midterm has replenished my motivation!

[andrewharley]

This just made my entire semester of Linear Algebra make a whole lot more sense.

[MinhTran-wnri]

@0:26 Think of an mxn matrix as a set of m row vectors (each with n elements) and a set of n column vectors (each with m elements).
@0:59 Matrix multiplication by a vector can be thought of as adding scaled column vectors together. The elements of the input vector tell how much to scale each column vector -- the first element tells how much to scale the first column vector, etc. The result of the multiplication is the vector you get having added the scaled column vectors together.
@1:17-1:33 A system of linear equations (which can be rewritten as matrix multiplication) can also be thought of as an intersection of planes. The output vector (the result of the matrix multiplication) determines where the planes of the equations lie. The point of intersection of those planes rerepresent the input vector. Intersection need not be a point, it can be a line or plane etc.
@2:06 Recap: A system of equations, which can be represented as matrix multiplication, can be thought of as intersecting planes or the sum of scaled column vectors. Intersecting planes help you solve for the input vector space (i.e., the set of all input vectors that makes the system equations equal). Sum of scaled column vectors help you visualize the image of the linear transformation (i.e., a mapping from the set of input vectors, the domain, to the image in the codomain).
@2:22 The set of all input vectors in the domain that map to the zero vector is called the nullspace (aka. kernel) of the linear transformation. It usually includes (0, 0, 0), the origin but the kernel could be a line, a plane, etc. @3:12 Gaussian elimination algorithm simplifies the system of equations to give you the kernel. @3:23 In gaussian elimination algorithm, when you multiply an equation by a constant, the plane changes shape but the part of the plane that is also a part of the kernel of the system of equations does not change. @4:13 If any two equations can be 'rotated onto' one another (forming a single indistinguishable plane), there is a 'free variable' which means the kernel space has moved up a dimension (i.e., a point to a line, a line to a plane, etc.). @4:55 The number of dependent variables are called pivots, the number of free variables indicate the dimension of the kernel (e.g., 1 free variable means the kernel has 1 dimension or in other words it has the shape of a line).
@5:26 A system of equations can be thought of as taking the inner product (i.e., dot product) of the input vector and each row vector. @5:53 when looking for the kernel (i.e., where the output vector is the zero vector), each equation in the system of equations is a constraint that says the kernel vector is perpendicular to the row vector. @6:10-6:44 The row vectors of the multiplication matrix span (i.e., the image of all linear combinations of the row vectors) a subspace that is perpendicular to the kernel.
@6:45-7:10 Each vector in the kernel contains elements that are scalars for the column vectors (of the transformation matrix) such that the scaled column vectors sum to the zero vector (i.e., the sum of the scaled vectors, put end to end, points back to the origin).
@7:10-7:25 Linearly dependent vectors. @7:25-7:51 Column space.
@8:11-8:22 The column space and the row space are always the same dimension.
@8:55-end Applications of matrix multiplication.

[natidadon]

Amazing!!
I just learned linear algebra at the University and yet I learned a few things from the video

[spacecase]

It’s because of you that my interest in math continues to grow daily

[maxgibbard]

I am amazed at how quickly this got complicated, yet it stayed digestible. The visual graphics complement the numbers and the vocals exquisitely. Great video!

[mehrosenasir]

the one thing that amazed me is when we scale a linear equation in Gauss Jordan elimination the point of intersection still remains the same. Just wow!!

[undeadarmy]

Amazing! Another video directly related to what I'm studying right now! Keep it up and maybe I won't have to study all semester. Thanks :)

[boluwarin]

You need to start a school. Everyone would sign up

[xariskatrisiosis]

Amazing work! I admire your passion! Your videos really inspire us.
This period of time I am studying about directional derivatives and gradients and I have to admit that they are difficult to understand. I know that this math section is absolutely essential for my other subjects. Could you please make a video about grads and directional derivatives because I want to learn the reasons why those things are so important and about their implementation in real life?
Thanks again about your help cause your videos are really helpful! I really appreciate it!

[douglasstrother]

As one gets further into mathematics and its applications, most problems boil-down to "Find the inverse of the matrix A." or "Compute the eigenvalues of the matrix A.", etc.

[soy-dave]

Great video! I wish this was introduced in my linear algebra class. It would have solidified the notion of "why" we were even doing Gaussian elimination in the first place as well as understanding the effect of what row reduced echelon form looks like. Keep it going!

[sfundomabaso]

This is beautiful to watch. I do wish I've seen it back when I was doing Linear Algebra, maybe my Quantum computing class would've been less confusing

[Jaojao_puzzlesolver]

This one video teaches me better than my linear algebra professor did for a full fkn year.
I don't even really need them when you and 3Blue1Brown doing so well.

[matattz]

Math can be so simple yet complicated at the same time. Once you visualize it, all makes perfect sense and you wonder why you didn’t grasp it sooner. Looking in your textbooks without these visual insights can be a really terrifying experience!

[smtxtv]

My Physics major in the 70s and 80s would have benefitted greatly by tutorials such as this, and YouTube and online resources in general. Great presentation !

[MrJaksld]

Thank you so much. I am literally taking linear algebra and was very confused by the null space. This video really helped especially the visualization