filmov
tv
Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra

Показать описание
How to think about linear systems of equations geometrically.
An equally valuable form of support is to simply share some of the videos.
Future series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
------------------
3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).
Various social media stuffs:
An equally valuable form of support is to simply share some of the videos.
Future series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.
Thanks to these viewers for their contributions to translations
Hebrew: Omer Tuchfeld
------------------
3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).
Various social media stuffs:
Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra
The Null Space & Column Space of a Matrix | Algebraically & Geometrically
Null space and column space basis | Vectors and spaces | Linear Algebra | Khan Academy
The Column Space of a Matrix
Column space of a matrix | Vectors and spaces | Linear Algebra | Khan Academy
1.6 Inverse matrices, column space and null space
Matrix Transpose and the Four Fundamental Subspaces
1.6 Inverse matrices, column space and null space (Cont.)
Arthur J Parzygnat: 'A generalization of inversion using Bayes' rule with applications to ...
Matrix Determinants ,Inverse , Rank , Column Space | Linear Algebra | Maths For Data Science
Dear linear algebra students, This is what matrices (and matrix manipulation) really look like
Null Space and Column Space of a Matrix
Order, Dimension, Rank, Nullity, Null Space, Column Space of a matrix
Part 1: The Column Space of a Matrix
Linear Algebra 11L5: The Column Space of AB
Nullspace Column Space and Rank
Column space of a matrix | Lecture 23 | Matrix Algebra for Engineers
Describing the Column Spaces (Lines or Planes) of these particular Matrices P 3-1-19
Find Null Space and Nullity of a Matrix | Linear Algebra
Finding Basis for the Column Space of a Matrix | Linear Algebra
Linear Algebra 8p: The Relationship Between the Column Space and the Null Space
Linear Algebra Column Space
4.7+8 Row Space, Column Space, Null Space, Rank & Nullity
Column Space of a Matrix Explained | Linear Algebra
Комментарии
 0:12:09
0:12:09
 0:10:41
0:10:41
 0:25:13
0:25:13
 0:12:44
0:12:44
 0:10:40
0:10:40
 0:11:21
0:11:21
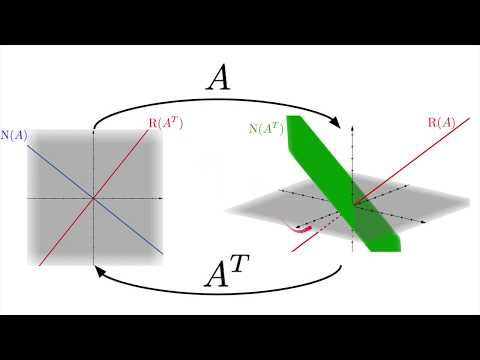 0:13:45
0:13:45
 0:08:35
0:08:35
 0:59:29
0:59:29
 0:12:16
0:12:16
 0:16:26
0:16:26
 0:07:51
0:07:51
 0:14:04
0:14:04
 0:14:00
0:14:00
 0:06:37
0:06:37
 0:20:59
0:20:59
 0:09:08
0:09:08
 0:05:16
0:05:16
 0:07:53
0:07:53
 0:03:59
0:03:59
 0:28:13
0:28:13
 0:00:56
0:00:56
 0:25:49
0:25:49
 0:14:22
0:14:22