filmov
tv
Find X (Lambert W Function - application)
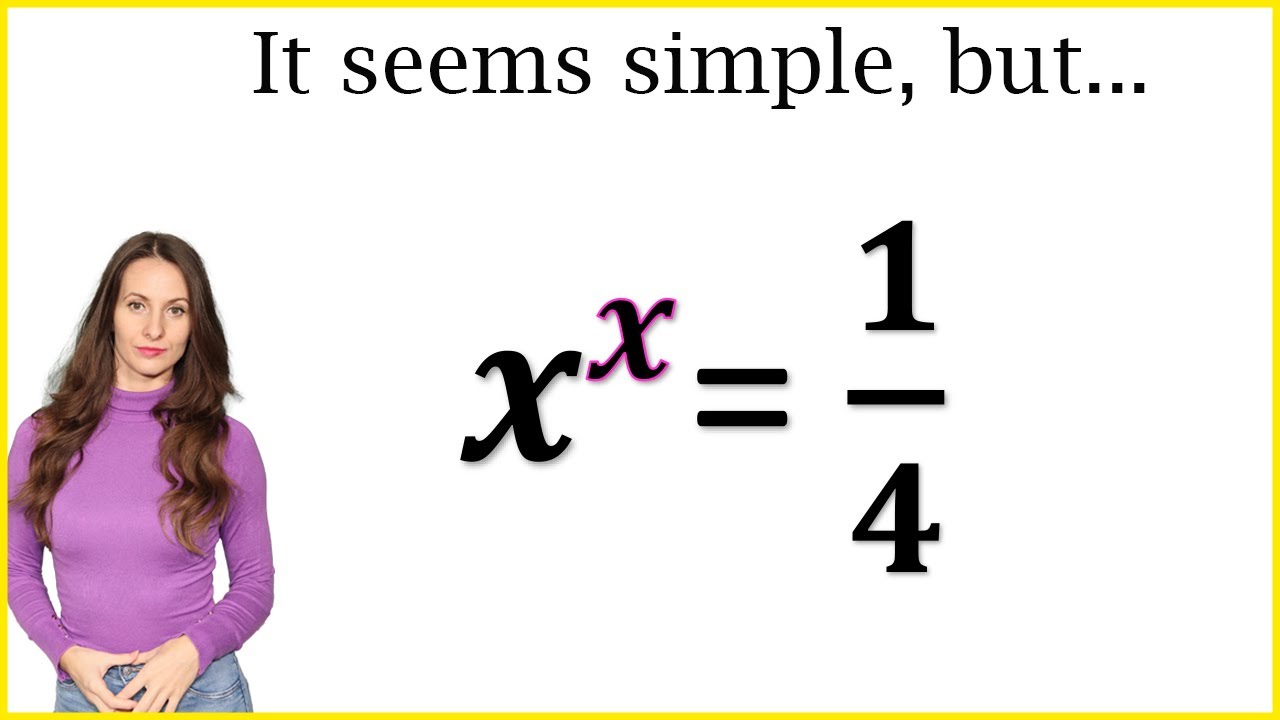
Показать описание
In this Video I am going to show you how to apply the Lambert W Function. I am explaining the basic tool when it comes to application of the Lambert W Function. Watching this Video you will be ably to recognize and solve some basic problems using the Lambert W Function.
If you want to see more videos like this, please like and SUBSCRIBE.
Don´t hesitate to click the ``BELL ICON`` next to the SUBSCRIBE button to be notified of UPLOADS.🔔
If you want to see more videos like this, please like and SUBSCRIBE.
Don´t hesitate to click the ``BELL ICON`` next to the SUBSCRIBE button to be notified of UPLOADS.🔔
Lambert W Function
Using the LAMBERT W FUNCTION find ALL solutions! / ( W_0 and W_-1)
Solving Exponential Equation (using Lambert W function)
Find X (Lambert W Function - application)
Lambert W Function (domain, range, approximation, solving equations, derivative & integral)
Simple Yet Difficult. How to Solve Using Lambert W Function
Awesome property of Lambert W function.
Lambert W Function Intro & x^x=2
Lambert W Function (No real solution???)
Introduction to the Lambert W Function
What is the Lambert W Function (Introduction )/ Part 1
How to Apply Lambert W Function To Solve Exponential Equations With Variables in the Base & Expo...
The Lambert W Function Introduction
Solving equations with lambert w function #shorts
Lambert W Function - Introduction
Lambert W Function solving exponential equations
if x+y=8, find the max of x^y (Lambert W function)
(PCb23) What is the Lambert-W Function?
How to find all solutions to the famous equation x^x=y^y (with Lambert W function)
Make your own Lambert W Calculator in a spreadsheet!
Math Olympiad Exam | Lambert W Function
Math Olympiad Problem | Challenging Algebra Problem | Lambert W Function | x^sqrtx =10 Finf x
Solving 8 Equations w/ Lambert W function
Find x using Lambert W function
Комментарии
 0:14:35
0:14:35
 0:25:14
0:25:14
 0:00:58
0:00:58
 0:04:43
0:04:43
 0:48:14
0:48:14
 0:03:39
0:03:39
 0:01:00
0:01:00
 0:10:01
0:10:01
 0:11:24
0:11:24
 0:10:41
0:10:41
 0:07:50
0:07:50
 0:10:20
0:10:20
 0:11:58
0:11:58
 0:01:00
0:01:00
 0:12:14
0:12:14
 0:06:06
0:06:06
 0:12:59
0:12:59
 0:09:41
0:09:41
 0:08:04
0:08:04
 0:15:10
0:15:10
 0:10:00
0:10:00
 0:05:27
0:05:27
 0:40:26
0:40:26
 0:09:00
0:09:00