filmov
tv
Solving Exponential Equation (using Lambert W function)

Показать описание
A Golden Exponential Equation Using Lambert W Function | Math Olympiad
A Nice Exponential Equation Using Lambert W Function
Lambert W Function solving exponential equations
Lambert W Function
Solving Exponential Equation (using Lambert W function)
Lambert W Function - solving exponential equations
Olympiad maths solving exponential equation using Lambert W function
Solving Exponential Equation 5^2x=7x Using Lambert Wn Function | Lambert w function introduction
Math Olympiad Exam | Lambert W Function | Solve Exponential Equation
How to Apply Lambert W Function To Solve Exponential Equations With Variables in the Base & Expo...
2 different exponential equations
Why I don't like using Lambert W function to solve exponential equation
You can solve unsolvable exponential equation 2x-4=2^x using Lambert W function.
Lambert W Function to Solve an Interesting Exponential Equation
Olympiad maths solving exponential equation using Lambert W function
Lambert W Function Versus Algebraic method In Solving Exponential Equations, Which Is Better?
Can you solve this exponential equation
Solving An Exponential with Lambert's W
How To Solve Exponential Equation x^5=9^x || Solving Exponential Equations.
A Tricky Exponential Equation e^(x)=ln(x) | Lambert W Function | Math Olympiad
The famous exponential equation 2^x=2x (ALL solutions)
Solving an exponential equation (the longer way)
Olympiad maths solving exponential equation using Lambert W function
Solving Exponential Equation Using Lambert W Function | y^5 = 9^y | Solve for y
Комментарии
 0:11:43
0:11:43
 0:07:59
0:07:59
 0:06:06
0:06:06
 0:14:35
0:14:35
 0:00:58
0:00:58
 0:04:40
0:04:40
 0:29:00
0:29:00
 0:10:06
0:10:06
 0:07:10
0:07:10
 0:10:20
0:10:20
 0:09:19
0:09:19
 0:03:32
0:03:32
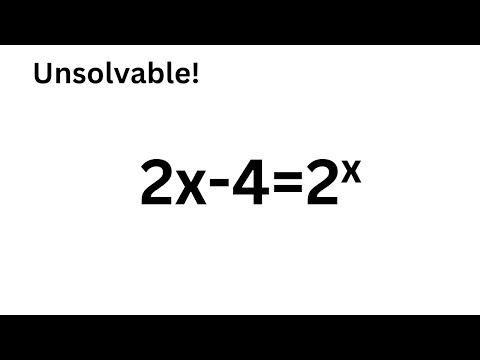 0:06:47
0:06:47
 0:02:36
0:02:36
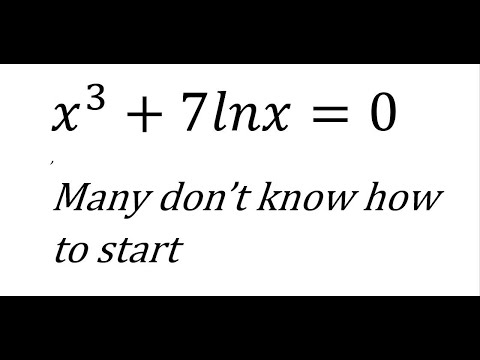 0:27:36
0:27:36
 0:09:12
0:09:12
 0:05:13
0:05:13
 0:08:56
0:08:56
 0:11:56
0:11:56
 0:05:30
0:05:30
 0:10:28
0:10:28
 0:04:43
0:04:43
 0:23:14
0:23:14
 0:12:35
0:12:35