filmov
tv
Let's Solve A Nice Factorial Equation
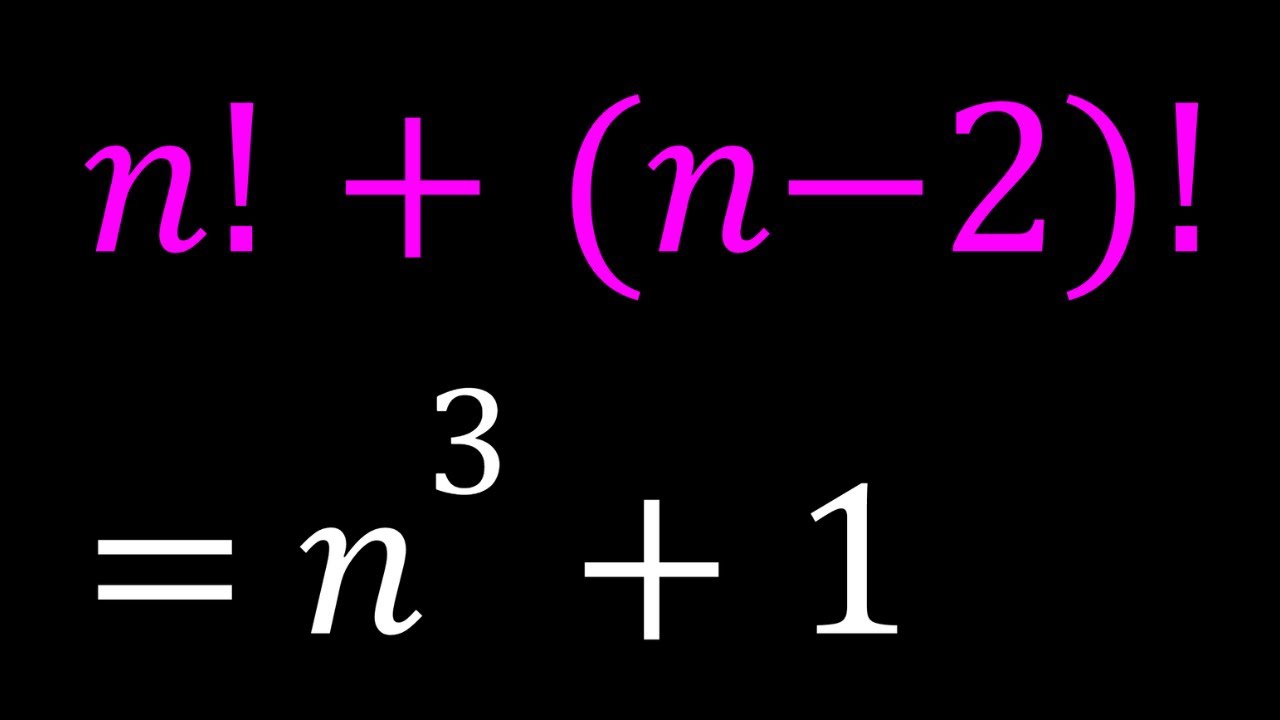
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries #sequence
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries #sequence
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Let's Solve A Nice Factorial Equation | Harvard-MIT
Let's Solve A Nice Factorial Equation
A Nice Factorial Math Problem? Can You Solve This?
Nice Factorial Equation - Can You Solve It?
a nice factorial problem
A nice factorial equation: The math behind solving equations.
A Nice Factorial Problem | Olympiad Question
A Nice Algebra Factorial Problem | Can You Solve This?
#27 Problem Solving Tutorial - 27 | Product of N natural no.'s - Factorial of a no. | Python
A Nice Math Problem On Factorial 👍 | You Should Learn This Method
A Nice Factorial Problem from Olympiad | Easy Step-By-Step Explanation
A Nice Factorial Math Simplification || Math Olympiad || Find the Value of X ||@TheMathScholar23
A Nice Math Problem with Factorial !
Can We Solve A Nice Factorial Equation
Solving A Nice Factorial Math Equation || Find the Value of n || Olympiad Math | n!@TheMathScholar23
Solving Nice Factorial Equation | Math Problem With Factorial
A Nice Factorial Problem from Olympiad | Easy Step-By-Step Explanation
Today: A Nice Algebra Olympiad Factorial Problem? Can You Solve This?
A Nice Factorial Problem from Olympiad | Easy Step By Step Explanation @mathsmood
A Nice Factorial Math Simplification || Math Olympiad || Find X || How to Solve @themathscholar23
Spain Math Olympiad Question | A Nice Factorial problem
what is the value of X ? | A nice factorial equation to solve
Math Olympiad Preparation | A Nice Factorial Problem | Calculate Without Calculators...
Nice Olympiad Mathematics problem|Olympiad Question| How to solve factorial
Комментарии
 0:10:56
0:10:56
 0:10:28
0:10:28
 0:03:05
0:03:05
 0:04:43
0:04:43
 0:00:37
0:00:37
 0:10:54
0:10:54
 0:04:28
0:04:28
 0:03:02
0:03:02
 0:06:16
0:06:16
 0:04:19
0:04:19
 0:03:03
0:03:03
 0:08:14
0:08:14
 0:02:03
0:02:03
 0:09:31
0:09:31
 0:06:04
0:06:04
 0:01:42
0:01:42
 0:05:12
0:05:12
 0:04:19
0:04:19
 0:02:29
0:02:29
 0:08:43
0:08:43
 0:01:19
0:01:19
 0:03:37
0:03:37
 0:06:19
0:06:19
 0:01:48
0:01:48