filmov
tv
A mysterious factorial equation.

Показать описание
We solve a nice equation over the natural numbers involving exponentiation and factorials. Our approach employs Wilson's theorem and other modular reduction tricks.
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
A mysterious factorial equation.
A Factorial equation: Simple but tricky #Shorts
The Mysterious Factorial Sequence
a nice factorial equation.
a nice factorial problem
Fun Factorial Fact
A strange factorial! #math #maths #factorial
How to Take the Factorial of Any Number
Mastering Factorial Equations: Solving a Challenging Example
how to solve a factorial equation?
The Secret Behind -1 Factorial
Solving the Unsolvable: Factorial Equation Challenge
Can You Beat the Odds? Factorial Equation Challenge!
A Nice Factorial Equation
Cracking Factorial Equations with Ease
Defeating Factorial Equations: Unveiling Effective Strategies and Solutions
Why is Pi here? | Half factorial without Gamma function #SoME3
Cracking the Factorial Mystery: Finding a in a! = a^3 - a
Solve factorial equation
Something Strange Happens When You Keep Squaring
Unlocking the Mystery of Zero Factorial: The Proof and Value of 0 Factorial Explained
Big Factorials - Numberphile
A Cool Factorial Equation | CAT Challenge
4 things you should know about factorial
Комментарии
 0:14:28
0:14:28
 0:00:40
0:00:40
 0:05:44
0:05:44
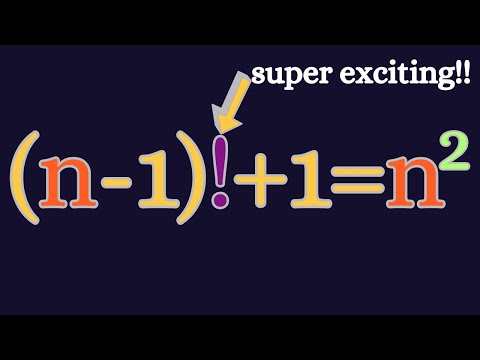 0:10:16
0:10:16
 0:00:37
0:00:37
 0:00:57
0:00:57
 0:00:51
0:00:51
 0:26:31
0:26:31
 0:09:00
0:09:00
 0:02:22
0:02:22
 0:05:03
0:05:03
 0:10:44
0:10:44
 0:10:00
0:10:00
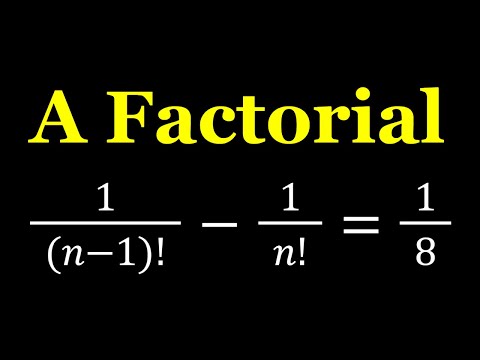 0:08:38
0:08:38
 0:08:52
0:08:52
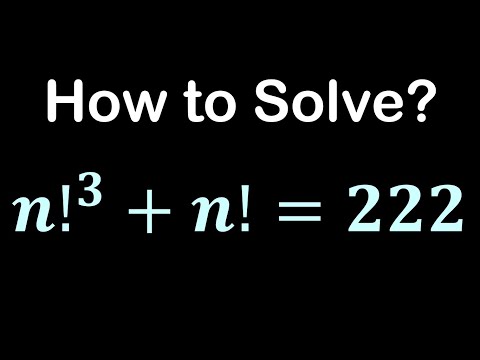 0:09:01
0:09:01
 0:13:14
0:13:14
 0:03:05
0:03:05
 0:06:31
0:06:31
 0:33:06
0:33:06
 0:06:18
0:06:18
 0:12:27
0:12:27
 0:12:41
0:12:41
 0:01:30
0:01:30