filmov
tv
A Nice And Perfect Factorial Equation

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you. ❤️ ❤️ ❤️
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries #sequence
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you. ❤️ ❤️ ❤️
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries #sequence
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
A Nice And Perfect Factorial Equation
What is a Factorial?
Can factorial sum be a perfect square ?
a nice factorial equation.
Factorial and Perfect Square --- Iran Math Olympiad 1995
A Factorial Perfect Square?
How to Solve Factorial Numbers #shorts
a super-factorial problem
Computer Architecture - Lecture 33: Cache Design and Management (Fall 2024)
A Nice Factorial Equation | Math Olympiad
Factors of factorial which are perfect square
A Very Nice Factorial Equation | Diophantine Equation | Math Olympiad Preparation
52-Card Perfect Shuffles - Numberphile
A Perfect Equation with Factorial
Factorial Simplification #maths
A Nice Math Problem with Factorial Expression #shorts #olympiad #maths #mathematics #short #tips #yt
A Nice Factorial Exponential Equation | Olympiad Math Prep!
Can factorial of a number be a perfect square ?
SSC CGL exam l Factorial Trick l How to solve Factorial Easily #math_trick #shorts Find factorial
A PERFECT SOLURUON TO FIND THE FACTORIAL OF A NUMBER IN C PROGRAMMING BROUGHT YOU BY DR HEINZ
Factorial Formula | Mathematics F.Sc (Part-1)|Exercise #7.1 |Maths by Muhammad Ahmad
#44 Python Program for calculate DOUBLE FACTORIAL using for loop#python#factorial#pythonforbeginners
Calculate factorial in C language #clanguage #coding #math
What’s 52 factorial ?
Комментарии
 0:05:26
0:05:26
 0:01:44
0:01:44
 0:02:57
0:02:57
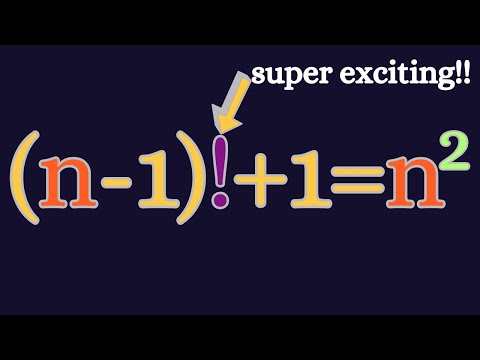 0:10:16
0:10:16
 0:06:29
0:06:29
 0:08:26
0:08:26
 0:00:56
0:00:56
 0:06:30
0:06:30
 2:26:20
2:26:20
 0:10:57
0:10:57
 0:08:22
0:08:22
 0:09:19
0:09:19
 0:09:34
0:09:34
 0:02:17
0:02:17
 0:00:22
0:00:22
 0:00:50
0:00:50
 0:08:36
0:08:36
 0:02:50
0:02:50
 0:00:15
0:00:15
 0:01:01
0:01:01
 0:00:16
0:00:16
 0:00:33
0:00:33
 0:00:53
0:00:53
 0:00:33
0:00:33