filmov
tv
Solving x^4=1

Показать описание
How to solve the 4th degree equation x^4=1? How many solutions does x^4=1 have? How do we solve x^4=1 by factoring? Can we just take the square root both sides for the equation x^4=1?
-----------------------------
-----------------------------
#math #algebra #mathbasics
-----------------------------
-----------------------------
#math #algebra #mathbasics
Solving x^4=1
solving x^4+1=0
Solving an equation with variables on both side and one solution
Solve quadratic equation by factorisation
Factoring a polynomial to the fourth power using factoring to second power
How to Solve One-Step Equations | One-Step Equation Steps | Math with Mr. J
Solve an equation for x by clearing fractions with multiple steps
A quartic equation solved in two ways! No quartic formula!!! x^4+4x-1=0
SOLVING PRETTY EASY EQUATION | 9^x=X^6
Solving A Very Special Quartic | x^4+1=0
Expanding Brackets
Solving Rational Equations
Solving an equation for y and x
solving equations but they get increasingly awesome
Strategies to Solve Multi Step Linear Equations with Fractions
5 simple unsolvable equations
Algebra - How To Solve Equations Quickly!
Solve a Linear Equation: 1/4x+1/2=2(4/5x+3)
Fractions Butterfly Method #Short Video #Maths
How to solve a 5-term 4th degree polynomial equation x^4+x^3+x^2+x+1=0
Solving x^x=4^{x+16}
9 TIMES TABLE #shorts #math #maths #mathematics
x+1/x Tricks for competitive exams | Algebra Questions for SSC CGL NTPC Railway Exams
Solving an equation using factoring, 4x^2 - 5x + 1 = 0
Комментарии
 0:04:56
0:04:56
 0:09:34
0:09:34
 0:02:36
0:02:36
 0:09:05
0:09:05
 0:03:26
0:03:26
 0:06:54
0:06:54
 0:03:44
0:03:44
 0:14:36
0:14:36
 0:01:36
0:01:36
 0:00:46
0:00:46
 0:00:51
0:00:51
 0:11:03
0:11:03
 0:03:47
0:03:47
 0:10:44
0:10:44
 0:15:41
0:15:41
 0:00:50
0:00:50
 0:25:05
0:25:05
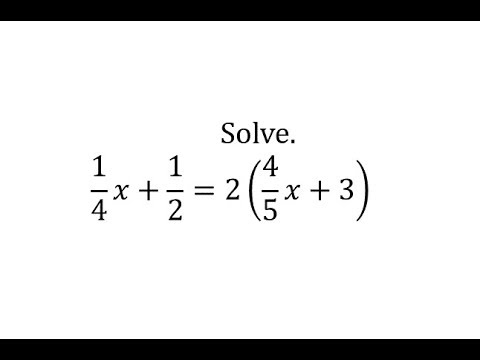 0:05:11
0:05:11
 0:00:27
0:00:27
 0:13:19
0:13:19
 0:09:16
0:09:16
 0:00:23
0:00:23
 0:00:24
0:00:24
 0:01:30
0:01:30