filmov
tv
Solving A Very Special Quartic | x^4+1=0
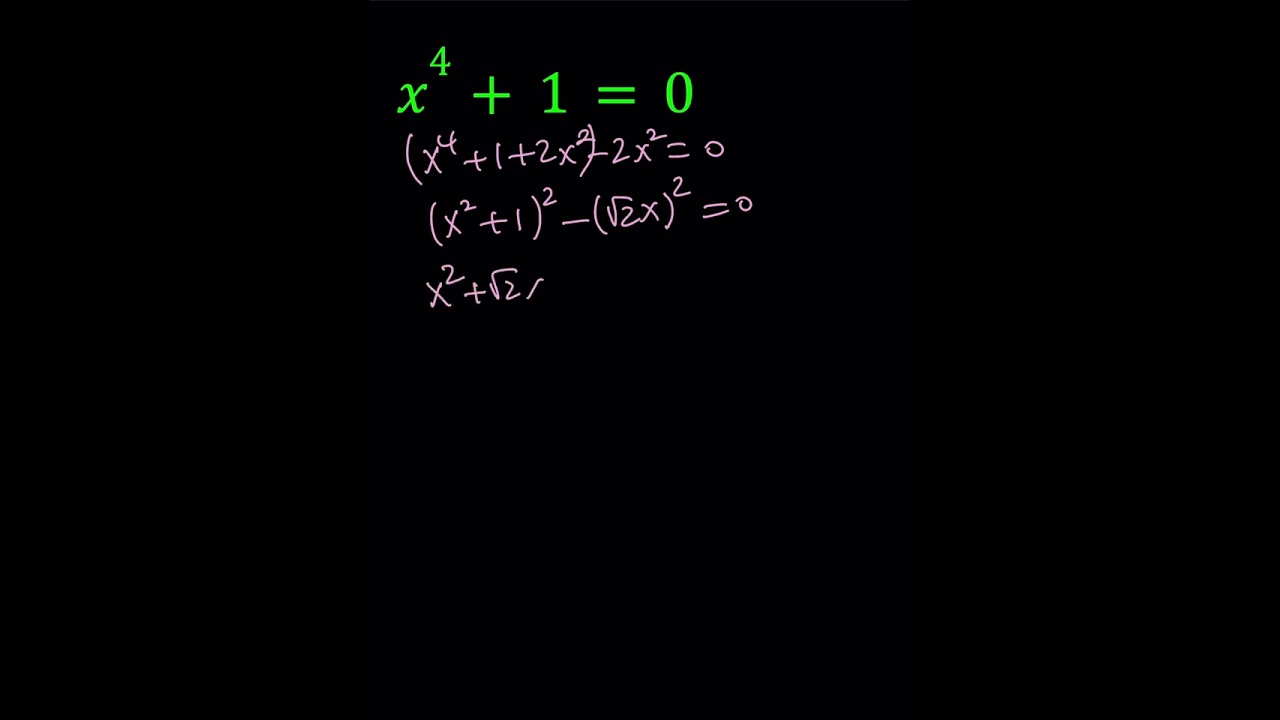
Показать описание
⭐ Join this channel to get access to perks:
#shorts #shortsvideo #shortsyoutube
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
#shorts #shortsvideo #shortsyoutube
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
Solving A Very Special Quartic | x^4+1=0
Solving A Special Quartic
Solving A Special Quartic | Generalization
A quartic equation, how to solve it? A special way makes it easy | Olympiad Math Practice
5 simple unsolvable equations
A Special Quartic Equation | No Quartic Formula
How to Solve Quartic Equation in Quadratic Form
The most fun way of solving this quartic equation
Solving a Quartic Equation with Quadratic Techniques
How To Solve The Quartic Equation?
How to solve the quartic equation by the Ferrari method?
A quartic equation that can be solved easily. No quartic formula needed.
Ukrainian Math Olympiad - Interesting Quartic Equation
Solving a Quartic Equation
When mathematicians get bored (ep1)
Classwiz How-To: Solving a Quartic Equation
Solving a Quartic Equation with Four Variables
Solving a Quartic Equation
solving equations but they get increasingly awesome
Solving A Special Quartic | x^4 - 12x =17
Lets Solve A Quartic Equation | Math Olympiads
Solving a Quartic with Four Variables | Algebra Challenge
Solving a quartic equation
The Quartic Formula (Ferrari's Method)
Комментарии
 0:00:46
0:00:46
 0:10:52
0:10:52
 0:08:48
0:08:48
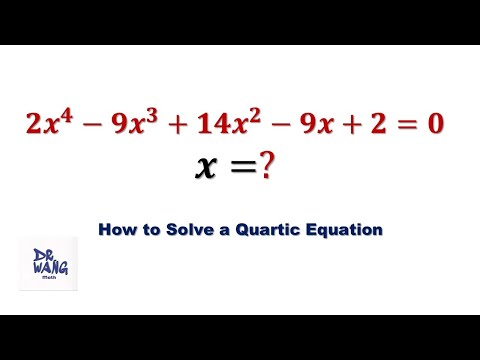 0:06:21
0:06:21
 0:00:50
0:00:50
 0:05:52
0:05:52
 0:02:33
0:02:33
 0:06:39
0:06:39
 0:06:57
0:06:57
 0:10:05
0:10:05
 0:13:19
0:13:19
 0:05:52
0:05:52
 0:08:08
0:08:08
 0:17:08
0:17:08
 0:00:37
0:00:37
 0:01:42
0:01:42
 0:09:46
0:09:46
 0:10:13
0:10:13
 0:10:44
0:10:44
 0:08:41
0:08:41
 0:08:55
0:08:55
 0:09:46
0:09:46
 0:00:49
0:00:49
 0:45:12
0:45:12