filmov
tv
Complex Exponentials to Solve the Laplace Transform of cos(at)
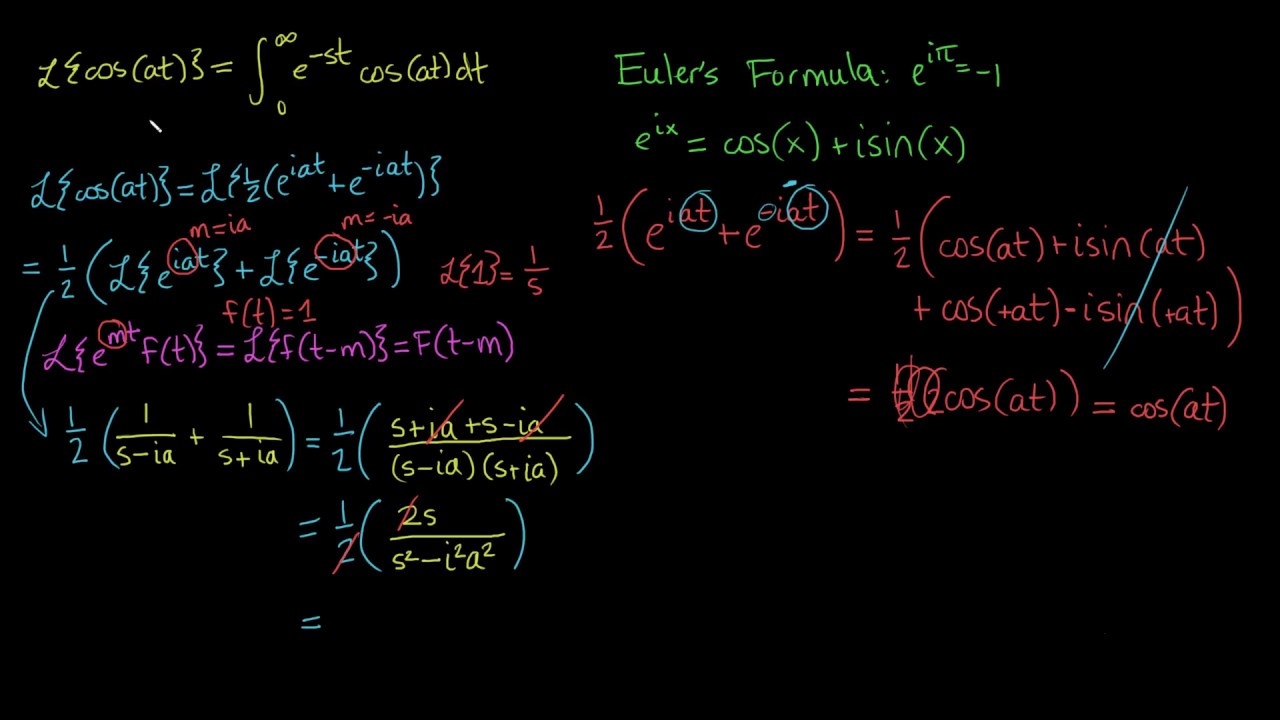
Показать описание
Typically, solving for the Laplace Transform of the sin(at) and the cos(at) involves two rounds of integration by parts. That isn't fun. The way to make it fun and much simpler is to rephrase the cosine function as a function of complex exponents with Euler's Formula. Then, several properties of the Laplace Transform make the solution short and sweet.
0:10:22
A Complex Exponential Equation with A Surprising Answer
0:04:08
e^(iπ) in 3.14 minutes, using dynamics | DE5
0:00:56
Solving Exponential Equation
0:11:53
Exponential form to find complex roots | Imaginary and complex numbers | Precalculus | Khan Academy
0:12:51
Response to Complex Exponential
0:00:53
What is a Complex Exponential?
0:00:54
Solving Exponential Equation
0:16:36
Solving Exponential Equations
0:03:36
Mastering Logarithmic Differentiation: Solving Complex Exponential Derivatives | d/dx[𝑎^(𝑎^𝑥 )]...
0:08:42
Eulers formula
0:05:58
Exponential Equations - Algebra and Precalculus
0:11:42
Complex Exponentials to Solve the Laplace Transform of cos(at)
0:04:30
Complex Analysis Episode 12: The Complex Exponential Function
0:00:22
Exponential Form to Logarithmic Form #Shorts #algebra #math #maths #mathematics #lesson #howto
0:00:33
The Euler's formula explained!
0:07:46
Rant: The Glory of Complex Exponentials
0:09:42
Complex Numbers - Exponential Form Examples : ExamSolutions Maths Tutorials
0:03:15
Exponential Form of a Complex Number
0:05:39
Transforming a Complex Number in to Exponential form
0:03:33
Can you solve this? | Exponential Equation | Algebra Problem.
0:07:19
Identity with the Complex Exponential - Complex Analysis Proof
0:07:55
Solving Complex Exponential Equations
0:11:21
Cosine and Sine Functions in terms of Complex Exponentials || Derivation from Euler's Formula
0:00:45
Absolute Value of Complex Number
Комментарии