filmov
tv
Quaternions as 4x4 Matrices - Connections to Linear Algebra
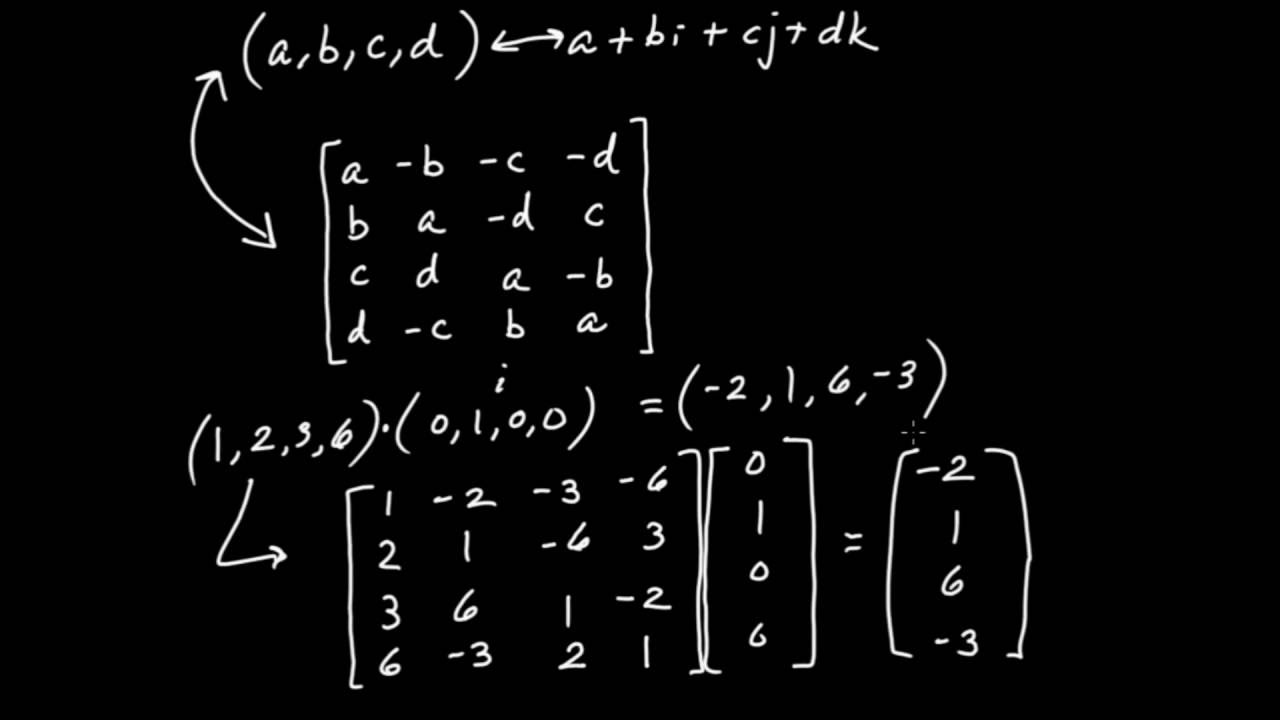
Показать описание
In math, it's usually possible to view an object or concept from many different (but equivalent) angles. In this video, we will see that the quaternions may be viewed as 4x4 real-valued matrices of a special form. What is interesting here is that if you know how to multiply matrices, you already know how to do more or less any calculation with quaternions. Moreover, we will see that the fundamental relations between the quaternionic imaginary units, i, j, and k also hold in matrix form.
If you enjoyed this video, please subscribe and leave comments!
If you enjoyed this video, please subscribe and leave comments!
Quaternions as 4x4 Matrices - Connections to Linear Algebra
Basic Intro to Quaternions for 3D Rotations
Deriving Quaternions from Complex Numbers and Split-Quaternions
Math in Game Development Summit: A Visual Guide to Quaternions and Dual Quaternions
Quaternions | Robotic Systems
Visualizing quaternions (4d numbers) with stereographic projection
Quaternion to Matrix calculation - ProgrammingTIL #194 3D Math 38 tutorial video screencast
How quaternions produce 3D rotation
9 | Quaternionen | Quaternion als reelle 4x4 Matrix
Operations with Quaternions
Set Theory (Part 14b): Quaternions and 3D Rotations
Quaternions & Matrices - CG Forge - Quick Tip
Rotation matrix, Quaternion, Euler angles, Rodrigues' rotation explained
Rotations about an Arbitrary Axis using Quaternions
2.3 Rotations in 3D
Lecture 18: Rotation and How to Represent It, Unit Quaternions, the Space of Rotations
Set Theory (Part 14c): More on the Quaternions
Flight Simulation . Quaternion Algebra . Quaternion Product
Why Quaternions Are Normalized for Rotations
Example of Quaternions
Let's remove Quaternions from every 3D Engine: Intro to Rotors from Geometric Algebra
Quaternion Basics
Number Theory: rotations and quaternions
The Quaternion Group
Комментарии
 0:14:50
0:14:50
 0:05:49
0:05:49
 0:16:28
0:16:28
 0:59:58
0:59:58
 0:11:02
0:11:02
 0:31:51
0:31:51
 0:04:34
0:04:34
 0:11:35
0:11:35
 0:05:44
0:05:44
 0:11:57
0:11:57
 0:52:22
0:52:22
 0:09:57
0:09:57
 0:32:12
0:32:12
 0:17:15
0:17:15
 0:11:14
0:11:14
 1:26:31
1:26:31
 0:30:10
0:30:10
 0:12:52
0:12:52
 0:02:27
0:02:27
 0:05:35
0:05:35
 0:16:48
0:16:48
 0:05:51
0:05:51
 0:10:33
0:10:33
 0:11:30
0:11:30