filmov
tv
Solving A Special Quartic | x^4 - 12x =17
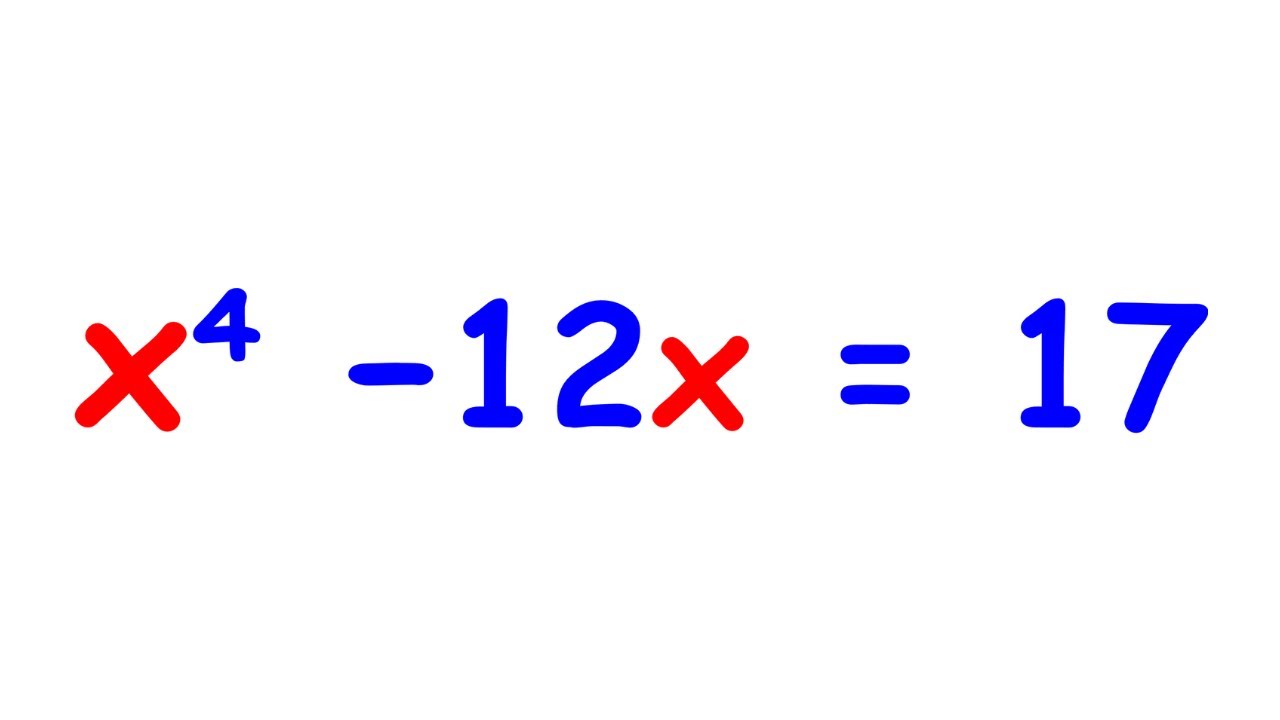
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
You can find ARML books and many others here. CHECK IT OUT!!! ❤️ ❤️ ❤️
❤️ Thanks to @NadiehFan for one of the methods!
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries #sequence
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
You can find ARML books and many others here. CHECK IT OUT!!! ❤️ ❤️ ❤️
❤️ Thanks to @NadiehFan for one of the methods!
If you need to post a picture of your solution or idea:
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries #sequence
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving A Special Quartic | x^4 - 12x =17
Solving A Special Quartic | Generalization
Solving A Special Quartic
A Special Quartic Equation | No Quartic Formula
A quartic equation, how to solve it? A special way makes it easy | Olympiad Math Practice
Solving A Very Special Quartic | x^4+1=0
A quartic equation that can be solved easily. No quartic formula needed.
Let's Solve A Special Type of Quartic
Solving a Quartic Equation
You probably haven't solved a quartic equation like this before!
Solving a Quartic Equation
The Quartic Formula (Ferrari's Method)
Cool Tricks for Solving a Quartic Equation!
you don't normally factor quartic #algebra #precalculus
Solving Quartic Equation!
Solving a quartic equation
A quartic equation is one where the greatest power is 4. Watch the full video to learn more! #maths
Cool trick for solving a quartic equation !
Solving A Quartic Equation | Two Methods
When mathematicians get bored (ep1)
Visual math every student should see quadratic formula
quartic equation / basic solution to solve quartic equation
Solving a quartic equation using an unusual idea. An algebraic challenge.
The most fun way of solving this quartic equation
Комментарии
 0:08:41
0:08:41
 0:08:48
0:08:48
 0:10:52
0:10:52
 0:05:52
0:05:52
 0:06:21
0:06:21
 0:00:46
0:00:46
 0:05:52
0:05:52
 0:10:56
0:10:56
 0:17:08
0:17:08
 0:12:59
0:12:59
 0:10:13
0:10:13
 0:45:12
0:45:12
 0:03:09
0:03:09
 0:00:34
0:00:34
 0:06:54
0:06:54
 0:07:46
0:07:46
 0:00:31
0:00:31
 0:00:51
0:00:51
 0:08:10
0:08:10
 0:00:37
0:00:37
 0:00:15
0:00:15
 0:05:25
0:05:25
 0:17:05
0:17:05
 0:06:39
0:06:39