filmov
tv
The Quartic Formula (Ferrari's Method)
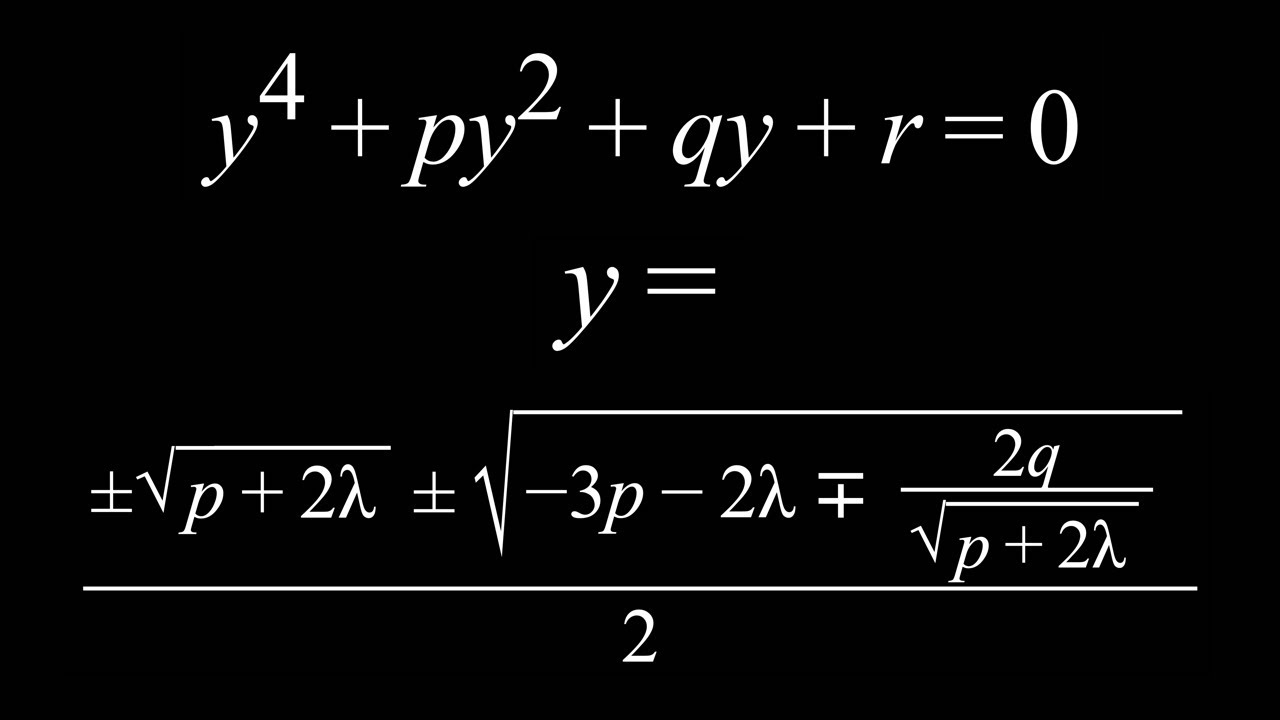
Показать описание
After finding the cubic formula using Cardano's method, the next step is to find the quartic formula using Ferrari's method. It is quite similar and builds on the ideas and concepts of Cardano's method with an extra step to form two perfect square quadratics.
Our journey for polynomial solution formulas in radicals ends here though since there is no formula for the quintic and higher degrees using elementary functions, but the methods to solve the quadratic, cubic, and quartic equation were definitely ingenious and worth the ride.
Timecodes:
0:00 - Intro and statement
0:35 - Formula derivation (choose λ s.t. p + 2λ ≠ 0 in the rare case)**
21:13 - Worked example
32:32 - Alternative steps in solving
34:26 - Extra on the discriminant
42:29 - Closing and unsolvability of the quintic
Sources and other tidbits:
Our journey for polynomial solution formulas in radicals ends here though since there is no formula for the quintic and higher degrees using elementary functions, but the methods to solve the quadratic, cubic, and quartic equation were definitely ingenious and worth the ride.
Timecodes:
0:00 - Intro and statement
0:35 - Formula derivation (choose λ s.t. p + 2λ ≠ 0 in the rare case)**
21:13 - Worked example
32:32 - Alternative steps in solving
34:26 - Extra on the discriminant
42:29 - Closing and unsolvability of the quintic
Sources and other tidbits:
The Quartic Formula (Ferrari's Method)
How to solve the quartic equation by the Ferrari method?
Ferrari and the Solution to the Quartic Equation
Quartic Equation using Ferrari's Method
How to solve Bi-Quadratic Equations (FERRARI method)
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
Solving Quartic equations using Ferrari's method.
FERRARI METHOD #2 - MATHEMATICS- HINDI
Lecture # 22 || Solution of Quartic Equation || Ferrari Method || Linear Algebra
FERRARI'S METHOD ||Solutions of Biquadratic equation.
Ferrari Method for Solving Bi-Quadratic equation
How to factor a hard 4th degree polynomial (no rational zero, can't do it by grouping)
FERRARI'S METHOD
Ferrari Method for Solving Bi-Quadratic Equation.
FERRARIS METHOD FOR SOLVING BIQUADRATIC EQUATION 🔥
068 - Solving Quartic Equations using Ferrari's Method - Practice
Ferrari Method for solving Bi-Quadratic equation 2
Ferrari Method Q.3- Mathematics
Ferrari method | Solving biquadratic/quartic equation by Ferrari's method | SEM 1 | Math Hons |...
4 DEGREE EQUATION SOLVED EASY PROCESS.. FERRARIS METHOD .. FOR CLASSICAL ALGEBRA.. FAST SOLUTION
Theory of Equation | Ferrari Method | Solution Of Bi-quadratic Equation
SOLUTION OF BIQUADRATIC EQUATIONS : Ferrari's Method | Analysis | BSc Mathematics
Bi-quadratic equn, Ferrari's method
Ferrari Method to solve Biquadratic Equation
Комментарии
 0:45:12
0:45:12
 0:13:19
0:13:19
 0:06:27
0:06:27
 0:15:07
0:15:07
 0:14:55
0:14:55
 0:36:58
0:36:58
 0:32:07
0:32:07
 0:08:02
0:08:02
 0:15:45
0:15:45
 0:04:36
0:04:36
 0:18:05
0:18:05
 0:04:55
0:04:55
 0:09:14
0:09:14
 0:18:47
0:18:47
 0:07:49
0:07:49
 0:43:30
0:43:30
 0:15:15
0:15:15
 0:09:57
0:09:57
 0:28:03
0:28:03
 0:11:41
0:11:41
 0:19:43
0:19:43
 0:14:11
0:14:11
 0:13:38
0:13:38
 0:12:26
0:12:26