filmov
tv
Solving A Special Quartic | Generalization

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving A Special Quartic | x^4 - 12x =17
Solving A Special Quartic | Generalization
Solving A Special Quartic
A Special Quartic Equation | No Quartic Formula
A quartic equation, how to solve it? A special way makes it easy | Olympiad Math Practice
Solving A Very Special Quartic | x^4+1=0
A quartic equation that can be solved easily. No quartic formula needed.
Solving a quartic equation without using the quartic formula. An algebra challenge
Solving a Quartic Equation
Let's Solve A Special Type of Quartic
How to Solve the Quartic Polynomial Equation?
Solving a Quartic Equation
You probably haven't solved a quartic equation like this before!
Cool Tricks for Solving a Quartic Equation!
Solving A Quartic | x^4+x^2+1=0 #maths
The Quartic Formula (Ferrari's Method)
Solving a quartic equation
A Symmetric Quartic Equation
Solving Quartic Equation!
Solving A Quartic Equation | Two Methods
you don't normally factor quartic #algebra #precalculus
Classwiz How-To: Solving a Quartic Equation
A quartic equation is one where the greatest power is 4. Watch the full video to learn more! #maths
I Solved A Quartic in Two Ways
Комментарии
 0:08:41
0:08:41
 0:08:48
0:08:48
 0:10:52
0:10:52
 0:05:52
0:05:52
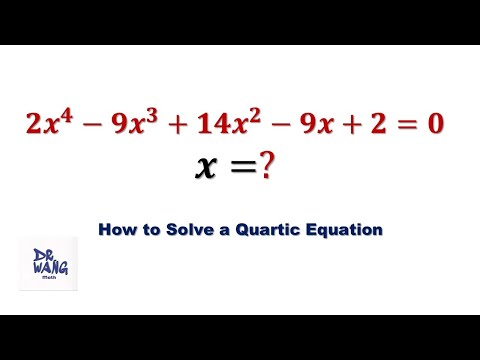 0:06:21
0:06:21
 0:00:46
0:00:46
 0:05:52
0:05:52
 0:03:52
0:03:52
 0:17:08
0:17:08
 0:10:56
0:10:56
 0:04:14
0:04:14
 0:10:13
0:10:13
 0:12:59
0:12:59
 0:03:09
0:03:09
 0:02:33
0:02:33
 0:45:12
0:45:12
 0:07:46
0:07:46
 0:07:47
0:07:47
 0:06:54
0:06:54
 0:08:10
0:08:10
 0:00:34
0:00:34
 0:01:42
0:01:42
 0:00:31
0:00:31
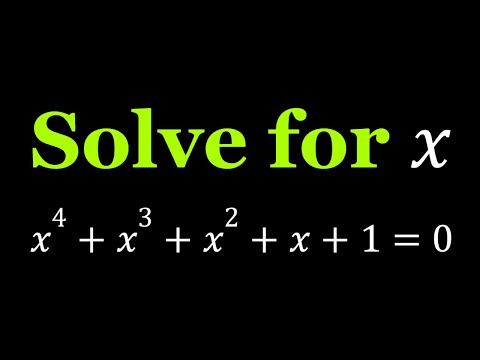 0:09:19
0:09:19