filmov
tv
What is 'above' the complex numbers??
Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
What is 'above' the complex numbers??
The beauty of complex numbers
Necessity of complex numbers
Complex analysis 101: imaginary numbers are real!
The complex number family.
Can you compare complex numbers?
15 - Complex Numbers & the Complex Plane
Complex numbers
Diamond Complex Fires over 6,000 acres
Problem Solving | Complex number basics.
Complex, Hermitian, and Unitary Matrices
Solving Equations With Complex Numbers
Factorisation with Complex Numbers
A nice algebra problem with complex numbers
Complex Numbers : The Argand Diagram : ExamSolutions
Factoring polynomials using complex numbers | Khan Academy
But, what ACTUALLY ARE Complex Numbers? - Complex Numbers, but Different [ Episode 7 ]
Complex integrals are ... different.
Complex Numbers - Division Part 1 | Don't Memorise
Complex numbers: Solving Equations (with example)
Linear Factorisation of Polynomials (1 of 2: Working in the Complex Field)
Algebra 2 - Simplifying complex numbers rational expression (2-4i) / (1+3i)
Who cares about complex numbers??
A surprising application of complex numbers in combinatorics #SoME2
Комментарии
 0:00:59
0:00:59
 0:13:42
0:13:42
 0:07:39
0:07:39
 0:00:21
0:00:21
 0:17:58
0:17:58
 0:15:22
0:15:22
 0:32:57
0:32:57
 0:08:36
0:08:36
 0:00:31
0:00:31
 0:34:14
0:34:14
 0:09:00
0:09:00
 0:02:07
0:02:07
 0:11:42
0:11:42
 0:10:50
0:10:50
 0:07:28
0:07:28
 0:03:10
0:03:10
 0:12:33
0:12:33
 0:14:12
0:14:12
 0:05:53
0:05:53
 0:16:06
0:16:06
 0:05:06
0:05:06
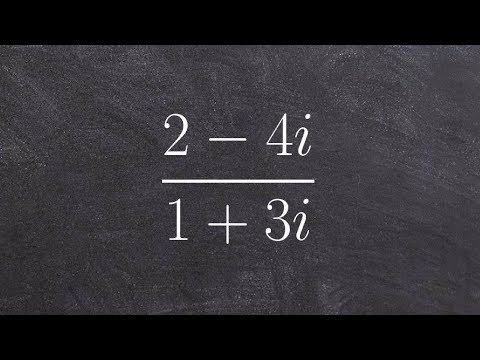 0:02:53
0:02:53
 0:13:53
0:13:53
 0:15:50
0:15:50