filmov
tv
Complex Numbers : The Argand Diagram : ExamSolutions

Показать описание
This video will explain how to tackle questions on complex numbers, specifically the argand diagram.
Complex Numbers : The Argand Diagram : ExamSolutions
Adding complex numbers and Argand Diagrams | Precalculus | Khan Academy
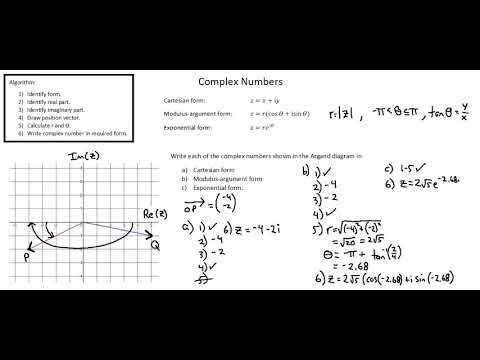
A-level Mathematics 9709: Argand diagrams and loci
Mathematics N4 The Argand Diagram _ Complex Numbers @mathszoneafricanmotives @mathswithadmirelighto...
What is Argand Plane? Part 1 | Complex Numbers | Don't Memorise
Represent Complex Number and Conjugate on Argand Diagram
A-level Mathematics 9709: Argand diagrams and representations of complex numbers part 1
Complex Numbers Argand Diagram Transformations
A-level Mathematics 9709: Argand diagrams and representations of complex numbers part 2
Complex Numbers - Plotting on an Argand Diagram
Plotting Complex Numbers on an Argand Diagram - Part 1 | Mr Mathematics
Complex Numbers - Transformations on the Argand Diagram
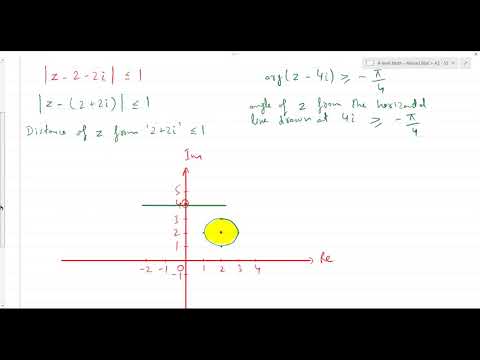
A-Level Further Maths B7-01 Argand Diagram: Introducing Loci for Circles |z-a|=r
Graphing Complex Numbers
P3 Complex Numbers | Argand Diagrams and Loci | Practice Questions (Part 1)
Complex Numbers : Modulus and Argument | ExamSolutions
Complex roots on Argand Diagram
Visualize unit complex numbers (rotation on Argand diagram)
What is a Complex Number
Complex Numbers 2 - Argand Diagram (Modulus and Conversion from one form to another)
P3 Complex Numbers | Argand Diagrams and Loci | Practice Questions (Part 2)
Multiplying Complex Numbers and the Argand Diagram
Complex Numbers: Shading an Argand Diagram
Complex Numbers In Polar - De Moivre's Theorem
Комментарии
 0:07:28
0:07:28
 0:04:39
0:04:39
 0:08:43
0:08:43
 0:08:09
0:08:09
 0:03:24
0:03:24
 0:03:46
0:03:46
 0:07:25
0:07:25
 0:18:32
0:18:32
 0:03:51
0:03:51
 0:05:47
0:05:47
 0:04:04
0:04:04
 0:13:32
0:13:32
 0:07:09
0:07:09
 0:01:51
0:01:51
 0:35:07
0:35:07
 0:16:50
0:16:50
 0:06:50
0:06:50
 0:00:56
0:00:56
 0:01:00
0:01:00
 0:42:44
0:42:44
 0:32:15
0:32:15
 0:03:16
0:03:16
 0:03:21
0:03:21
 1:04:47
1:04:47