Problem Solving | Complex number basics.

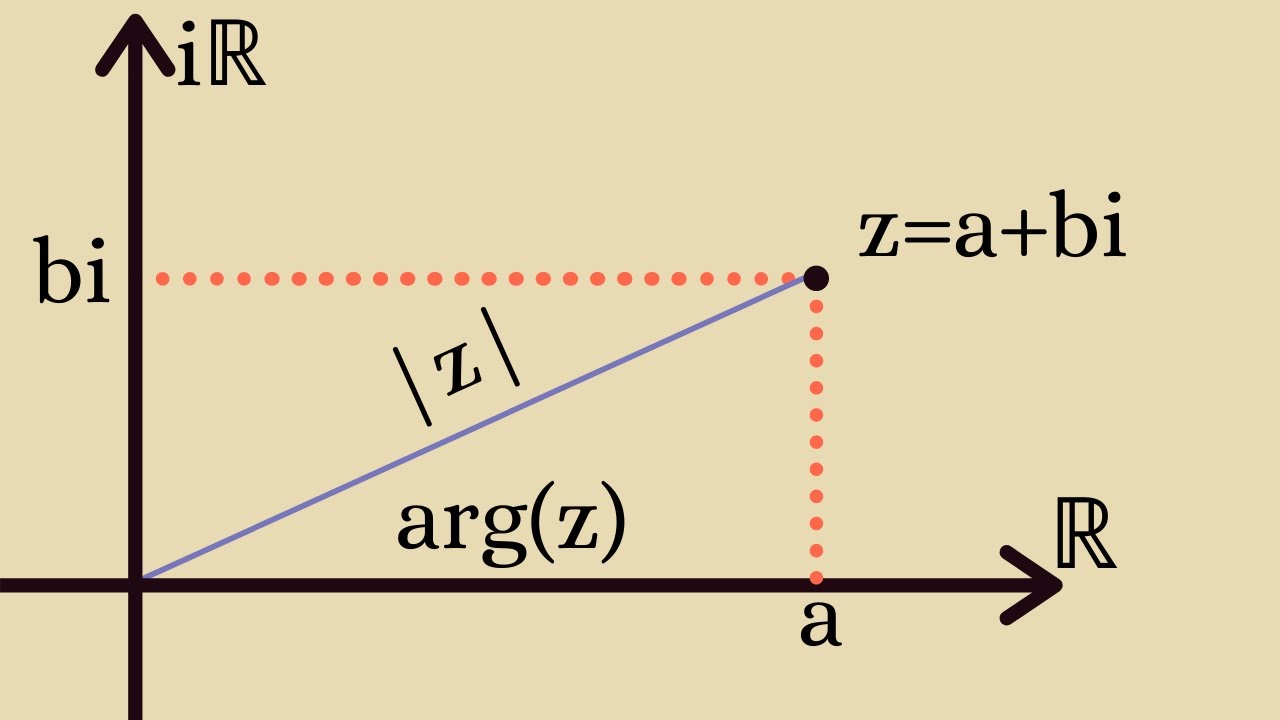
We look at some basic tools involving complex numbers for problem solving contests.

If you are going to use an ad-blocker, considering using brave and tipping me BAT!

Books I like:

Abstract Algebra:

Differential Forms:

Number Theory:

Analysis:

Calculus:

My Filming Equipment:

[madladphy]

Are you planning a complex analysis course on the channel? Would absolutely love it

[virajagr]

32:05 it should be zeta² Q(1) not zeta Q(1) although answer is still same

[alperenkoken]

Could you make problem solving videos about geometry bashing(vector, bary, inversion...)?

[goodplacetostop]

34:10

Hello Michael, hello everyone, what’s up? I have one suggestion for Mr Penn AND one homework for viewers.

Suggestion is from IMO 1997 short list.
Do there exist functions f and g (both R -> R) such that :
1. f(g(x))=x^2 and g(f(x))=x^3 for all x in R ?
2. f(g(x))=x^2 and g(f(x))=x^4 for all x in R ?

Homework : Choose three random real numbers X1, X2 and X3 from the interval [0;1], independently of each other.

1. What is the probability that X1 is stricly bigger than X2 + X3?
2. In general, what is the probability that the largest of the three random numbers is strictly greater than the sum of the other two?
3. Bonus (the source only gives the answer but not the whole explanation) : for X1, X2... Xn chosen in the same conditions (n bigger or equal than 2), what is the probability than X1 > X2 + ... + Xn

[MarieAnne.]

At around 32:00, when equating −P(1) = ζQ(1) + ζ²R(1) = ζ³Q(1) + ζR(1),
we should end up with Q(1) + ζR(1) = ζ²Q(1) + R(1).
Solving for R(1) gives R(1)(1-ζ) = Q(1)(1-ζ²) or *R(1) = Q(1)(1+ζ)* [not R(1) = Q(1)]
Plugging into previous equation Q(1) + ζR(1) = ζQ(1) + ζ³R(1) we get:
Q(1) + Q(1)ζ(1+ζ) = ζQ(1) + Q(1)ζ³(1+ζ)
Q(1)(1+ζ+ζ²) = Q(1)(ζ+ζ³+ζ⁴)
Q(1)(1+ζ²−ζ³−ζ⁴) = 0
Now the same argument can be made, but with a different expression.
Since 1+ζ²−ζ³−ζ⁴ ≠ 0, then *Q(1) = 0* → Q(1)(1+ζ) = *R(1) = 0*
We can then proceed to show that P(1) = 0 as shown in the video.

[maxxis]

I've just started working with complex numbers, great video!

[quantabot]

Yes!! I would love to see a complex analysis playlist....it would be just amazing

[captainsnake]

30-minute video + michael penn + complex numbers!?

Hey Ferb, I know what we're gonna do today

[funkyu]

would be epic if you covered contour integration and some theory behind that

[noumaneelgaou]

We can in simple method we have polynomials P(1)+XQ(1)+X^(2)R(1) has 3 different root then this polynomials is nule then P(1)=Q(1)=R(1)=0

[bamonroe]

This is great thanks! I was looking for some examples of patterns that look unsolvable with real numbers, but become solvable with complex numbers, like the sum of squares problem you explain starting at 18:30.

[abdlazizlairgi]

Best teacher ever I've learned many things from you, thanks

[dimitrisandroid]

More problem solving videos with basic theory please!

[hellosquirrel]

I wanted a video like this since so long ! Thank you so much :3

[mijmijrm]

what i think is cute about complex number is: it's simple to create integer hypotenuse rt triangles.
Eg. (2j1)^2 = 3j4 <- 3 4 5 triangle
(3j2)^2 = 5j12 <- 5 12 13 triangle
(4j1)^2 = 15j8 <- 15 8 17 triangle
etc

[cauchy]

Just amazing I was need this video so much thank u you are the best

[mathsaddict]

what is the easiest way of contacting you, professor?

[nuclo]

I dont get it. P(1)=0 implies automatically P(X)=(X-1)A(X) where A is a polynomial, if P is a polinomial. Isnt that trivial ?

[rikhalder]

Please tell what's difference between norm and modulus

[roberttelarket]

The powers that be need to eliminate the words imaginary numbers and complex numbers once and for all!
Their presentation should be by dyads as taught correctly in modern abstract algebra.