filmov
tv
Complex integrals are ... different.

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟Suggest a problem🌟
Complex integrals are ... different.
Complex integration, Cauchy and residue theorems | Essence of Complex Analysis #6
Complex Analysis L12: Examples of Complex Integrals
Visualizing Complex Integrals
Complex Integrals | Contour Integration | Complex Analysis #11
Complex Analysis L08: Integrals in the Complex Plane
Complex Analysis - Computing Line Integrals
Complex Integrals and Cauchy's Integral Theorem.
MAT3705 UNISA|Complex Analysis|Applications of Residues|Contour Integration|Multiple-Valued Function
how to solve these HARD integrals
Necessity of complex numbers
Complex Integration and Finding Zeros of the Zeta Function
What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2
Integrals: degree of top GREATER than bottom. #calculus #integrals #mathchallenge #mathtricks
Complex Analysis #4 | Complex line integrals
Contour Integrals
Complex Analysis - Line Integrals
Introduction to contour integrals on complex plane
These integrals all equal π, until...
two vibin complex integrals
Evaluating Real Integrals Part 2 | Improper Integrals | Complex Analysis #19
i did another 100 integrals!
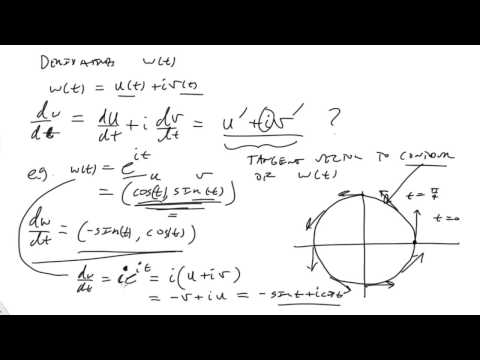
Derivatives and integrals of complex functions w(t)
Line Integrals. #calculus
Комментарии
 0:14:12
0:14:12
 0:40:45
0:40:45
 0:21:34
0:21:34
 0:09:02
0:09:02
 0:14:05
0:14:05
 0:41:29
0:41:29
 0:07:03
0:07:03
 0:07:57
0:07:57
 2:04:51
2:04:51
 0:09:45
0:09:45
 0:07:39
0:07:39
 0:52:49
0:52:49
 0:22:40
0:22:40
 0:00:48
0:00:48
 0:16:46
0:16:46
 0:26:09
0:26:09
 0:20:37
0:20:37
 0:23:17
0:23:17
 0:00:51
0:00:51
 0:11:47
0:11:47
 0:17:01
0:17:01
 0:00:16
0:00:16
 0:19:05
0:19:05
 0:00:51
0:00:51