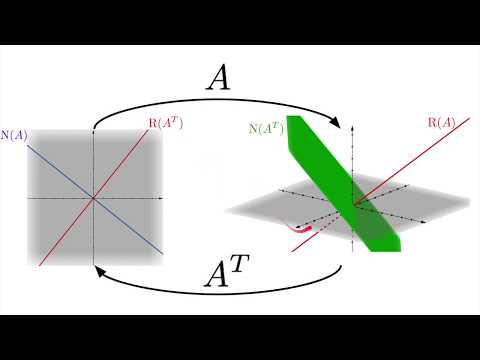
Matrix Transpose and the Four Fundamental Subspaces

Geogebra (Used for making plots):

Notes
[1] By "gives a sense", I mean contains vectors that can form an orthogonal basis for the components of the vectors not in the ranges.
[2] It isn’t really legal to plot R^2 and R^3 on the same set of axes like this, R^2 and R^3 are completely different spaces, but I’m showing them like this to provide some intuition and justification for all three parts of the SVD.

[martinbiroscak]

This solved about 5 years of my confusion in 10 minutes. Thank you so much.

[Kralasaurusx]

I love how geometric and intuitive this explanation is. It seems as though a lot of math lectures and explanations often end up deep into the symbols that the higher-level intuition and meaning gets lost. Not that symbolic explanations are bad per se, but it definitely helps to be able to understand and visualize things at a high level like this. Thanks for the excellent explanation.

[jarthur]

How the hell you only have 13 subs.... Is one of the best explanation I ve found!!!!

[njt]

The best explanation of transpose matrix on the internet. Very clear voice and simple visualizations!

[moseschuka]

Super helpful, this is not usually explained in textbooks. Authors just assume you know what is happing. Couldn't find better explanation elsewhere. Thanks a lot.

[speedbird]

Thank you sir,
You really provided a good visualization for how matrices distort/stretch data. A_transpose and A_dodge rotate the date in same manner but magnify differently! Visually, since they have the same rotational effects, the orientations of the basis vectors does not change, so their subspaces, particularly the null space and column(range) spaces remain intact. But still A_transpose and A_dodge distort data shapes differently!

[madeautonomous]

This is really good, thank you so much. Was confused by the fundamentals of subspaces and what do they mean in terms of visualization.

[harryhuang]

Amazing job Ben. Explained with such conciseness and clarity

[ETeHong]

What an incredible video you uploaded!

[varunsharma]

Loved IT. Best video on transpose on youtube.

[forthrightgambitia]

I just realised, the U and V in SVD are *transformation of basis* matrices, which is why applying the inverse sends it to the x/y plane. The only part I don't understand is why V^T maps it to be under U in the x/y plane.

[christophercrawford]

Nice geometric intuition.

Note that the SVD actually rotates the image and coimage from/to the x axis (or xy-plane, etc) so the diagonal matrix can do its job. In general, 'rotation into the same direction as the image' is not well-defined.

You could extend your intuition to motivate A+ = (A^T A)^-1 A^T, since A^T A maps the image back to the image, swished around.

[meharjeetsingh]

Thank You Ben! It was a lovely experience watching your video.

[hideyoshitheturtle]

3:10 “Applying A squishes R^2 like this” doesn’t click in my head. The matrix A is a mapping from R^2 to R^3, so I’m not sure why the output vector is discussed in R^2 instead of R^3…?

[nitinjain]

You are the only one who is clearing this transpose doubt....i understand few things here

But there is one doubt

While you explaining the both range on same space through the example

I didnt get the point why the vector length on R(A+) is different from R(A)

Could you clear this doubt ?

I know it will be not easy in text to explain but if you can with same video you can include example in more defined way

Really thanks for this video i learned a bit more today

[meharjeetsingh]

Can you also explain the difference between transpose(A) and inverse(A)?

[minhducphamnguyen]

I understand up to the point where you're breaking down how to transform the R(A+) subspace to the R(A) subspace. Why does the 1st rotation V^T have to be orthogonal?

[pauselab]

A homomorphic function maps K^n to K^m sending each element of K^n to a subspace of K^m.
A^T the transpose maps K*^m to K*^n sending each element of K*^m to a subspace of K*^n. where K* is the dual space of K and it must satisfy A^T(f)= f(A), f is a linear transformation in A^T.

the 4 spaces are the kernel and the image of A and A^T. now it happens that K is always isomorphic to K* if both n and m are finite natural numbers. so you can kind of think of A^T as a function from K^m to K^n.

in the example:
A maps R^2 to a line in R^3, ima(A) and ker(A) are both lines.
A^T maps R*^3 to a line in R*^2, ima(A^T) is a line and ker(A^T) is a plane.

[adityanjsg]

Too overlooked channel.
Instant sunscribe!

[prashantgupta]

Wow.... Superb VIdeo.... Best video ever seen.. : 11:06