filmov
tv
Solving A Nice Differential Equation
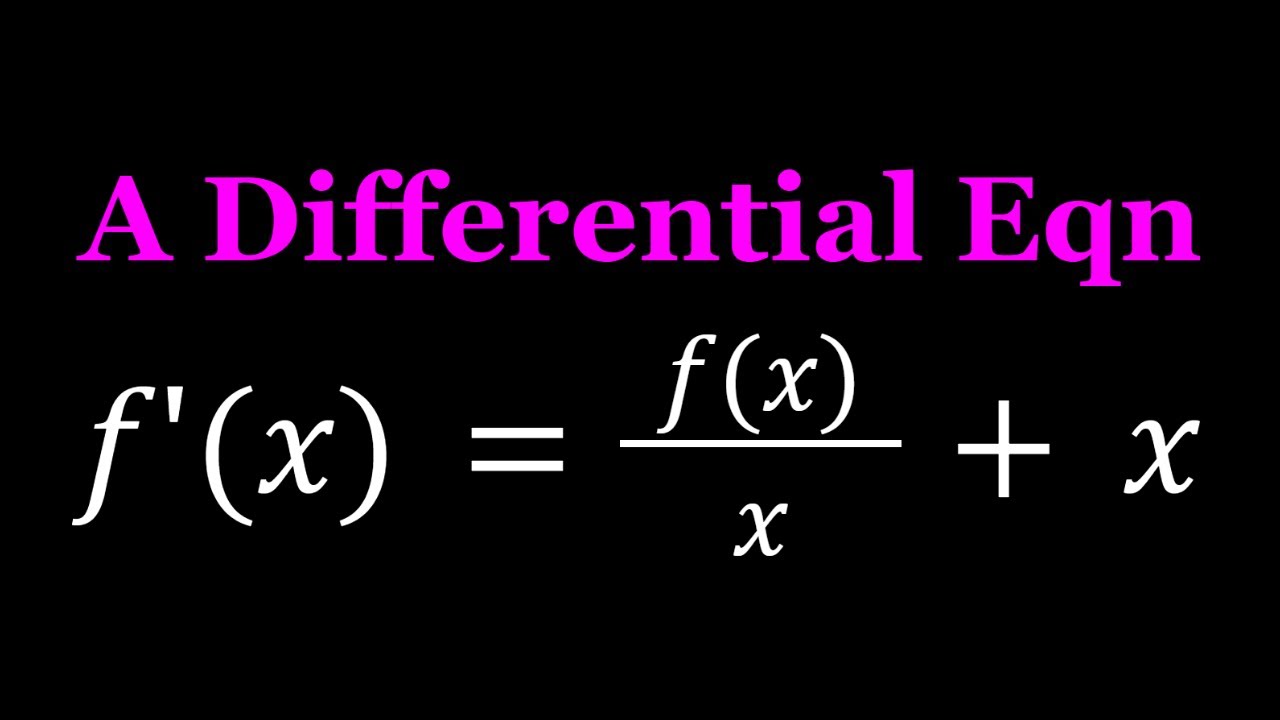
Показать описание
If you need to post a picture of your solution or idea:
#CalculusProblems #DifferentialEquations
PLAYLISTS 🎵 :
#CalculusProblems #DifferentialEquations
PLAYLISTS 🎵 :
Solving A Nice Differential Equation
not {linear, separable, exact}, but solvable -- a nice differential equation.
One Nice. Differential Equation
Nice tricks to solve this Differential Equation.
4 Types of ODE's: How to Identify and Solve Them
Separable First Order Differential Equations - Basic Introduction
How to solve ANY differential equation
A nice suggested differential equation
Math Olympiad Question | Algebra Equation Solving | international math olympiad questions #olympiad
Differential equations, a tourist's guide | DE1
Edexcel A level Maths: 11.10 Solving Differential Equations (Part 1)
Differential equation introduction | First order differential equations | Khan Academy
First Order Linear Differential Equations
First order, Ordinary Differential Equations.
First Order Linear Differential Equation & Integrating Factor (introduction & example)
This is why you're learning differential equations
Solving A Differential Equation | Two Methods
How to Solve Differential Equations in PYTHON
Non-linear differential equations have strange solutions!
How to determine the general solution to a differential equation
Solving an Exact Differential Equation
Calculus 2 Lecture 8.1: Solving First Order Differential Equations By Separation of Variables
Physics Students Need to Know These 5 Methods for Differential Equations
Solving a Homogeneous Differential Equation
Комментарии
 0:09:28
0:09:28
 0:04:43
0:04:43
 0:10:55
0:10:55
 0:06:48
0:06:48
 0:06:57
0:06:57
 0:10:42
0:10:42
 0:05:05
0:05:05
 0:11:41
0:11:41
 0:00:59
0:00:59
 0:27:16
0:27:16
 0:14:07
0:14:07
 0:07:49
0:07:49
 0:22:28
0:22:28
 0:48:35
0:48:35
 0:20:34
0:20:34
 0:18:36
0:18:36
 0:12:18
0:12:18
 0:23:37
0:23:37
 0:13:46
0:13:46
 0:02:03
0:02:03
 0:02:46
0:02:46
 2:49:22
2:49:22
 0:30:36
0:30:36
 0:08:40
0:08:40