filmov
tv
Nice tricks to solve this Differential Equation.
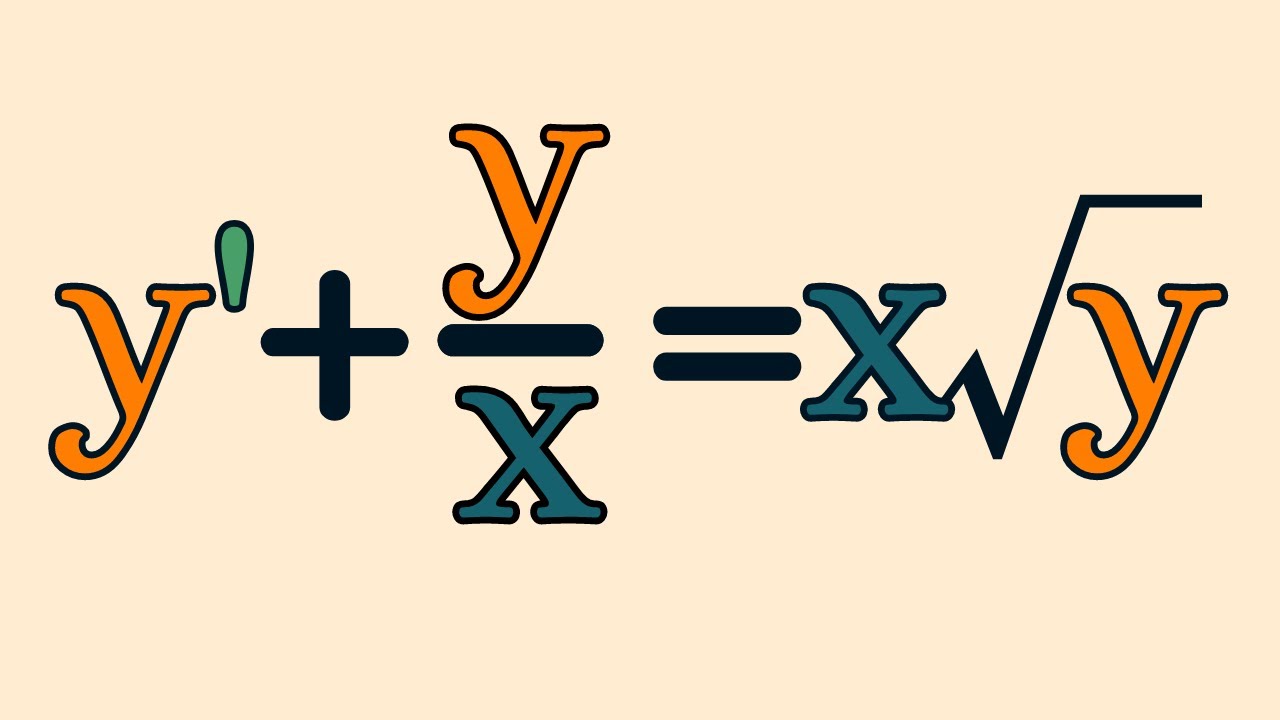
Показать описание
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
My Filming Equipment:
Nice tricks to solve this Differential Equation.
10 Tips to Solve the Rubik's Cube in 30 Seconds!
3 Tips on solving the Rubik’s cube
3 by 3 rubik's cube solve magic tricks 😈...#viral #shorts #shortsvideo
Magic tricks to solve Rubik's Cube (2×2)#Shorts
Nobody Believes But It Really Works!! 17 Brilliant Home Tricks + 5 Tips That Work BETTER Than Magic
Arithmetic Tricks - solve tedious math problems in no time
Rubik's Cube: 7 Tips For An Efficient Cross Every Solve (CFOP)
3 Tips To Solve A Rubik's Cube In 8 Seconds 🌟
Easy Tips And Tricks to Solve 3x3 Rubik's Cube in Under 1 Minute!
How To Solve Rubik’s Cube 3x3 - Cube Solve Magic Trick Formula #shorts
😳 computer hanging 100% solution 👍| #shorts #tricks #computer #tech
Solve This ANNOYING F2L Case Rotationless - F2L Tips #9
How to Solve Number Analogy Question Reasoning Short Tricks | #reasoning short tricks
Easily 3 Star No Strings Attached Challenge (Clash of Clans)
🔥Hair growth tips/hair fall solution at home #hairgrowth #hairfall #haircare #viral #short #shorts...
Magical tricks to solve 3/3 Rubik's cube #puzzle #youtubeshorts #trending
Rubiks cube solve new magic tricks #shorts #tre
Rubik's cube tricks to solve Rubik's cube #rubikscube #rubikscubesolve #shorts #youtubesho...
Solve this ANNOYING F2L Case Rotationless - F2L Tips #1
TRICKS CUBE SOLVE PERFECT SOLVE #perfect #easily #wonderful #shortvideo
Maths puzzle tricks only genius can solve 💯 # shorts # shortsvideo # YouTube shorts
The engine shakes abnormally, free solution(4) #driving #drivetips #automobile#diy #tips #car
How to Solve Riddles - 5 Great Tips and Tricks
Комментарии
 0:06:48
0:06:48
 0:10:43
0:10:43
 0:00:29
0:00:29
 0:00:11
0:00:11
 0:00:32
0:00:32
 0:11:15
0:11:15
 0:01:23
0:01:23
 0:10:00
0:10:00
 0:09:59
0:09:59
 0:06:38
0:06:38
 0:00:19
0:00:19
 0:00:26
0:00:26
 0:00:43
0:00:43
 0:00:59
0:00:59
 0:02:35
0:02:35
 0:00:18
0:00:18
 0:00:50
0:00:50
 0:00:23
0:00:23
 0:00:21
0:00:21
 0:00:29
0:00:29
 0:00:18
0:00:18
 0:00:12
0:00:12
 0:00:37
0:00:37
 0:06:58
0:06:58